题目内容
证明三角恒等式2sin4x+
sin22x+5cos4x-cos3xcosx=2(1+cos2x).
| 3 |
| 4 |
证明:左边=2sin4x+
(2sinxcosx)2+5cos4x-cos(2x+x)cosx
=2sin4x+3sin2xcos2x+5cos4x-(cos2xcosx-sin2xsinx)cosx
=2sin4x+3sin2xcos2x+5cos4x-[(2cos2x-1)cosx-2sin2xcosx]cosx
=2sin4x+3sin2xcos2x+5cos4x-[2cos3x-cosx-2(1-cos2x)cosx]cosx
=2sin4x+3sin2xcos2x+5cos4x-(4cos3x-3cosx)cosx
=2sin4x+3sin2xcos2x+cos4x+3cos2x
=(2sin2x+cos2x)(sin2x+cos2x)+3cos2x
=2sin2x+cos2x+3cos2x
=2+2cos2x=2(1+cos2x)=右边
| 3 |
| 4 |
=2sin4x+3sin2xcos2x+5cos4x-(cos2xcosx-sin2xsinx)cosx
=2sin4x+3sin2xcos2x+5cos4x-[(2cos2x-1)cosx-2sin2xcosx]cosx
=2sin4x+3sin2xcos2x+5cos4x-[2cos3x-cosx-2(1-cos2x)cosx]cosx
=2sin4x+3sin2xcos2x+5cos4x-(4cos3x-3cosx)cosx
=2sin4x+3sin2xcos2x+cos4x+3cos2x
=(2sin2x+cos2x)(sin2x+cos2x)+3cos2x
=2sin2x+cos2x+3cos2x
=2+2cos2x=2(1+cos2x)=右边

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
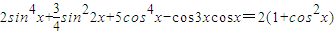 .
.