题目内容
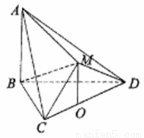
如图,在多面体 中,△
中,△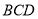 是等边三角形,△
是等边三角形,△ 是等腰直角三角形,
是等腰直角三角形,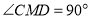 ,平面
,平面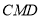 ⊥平面
⊥平面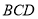 ,
,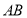 ⊥平面
⊥平面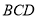 ,点
,点 为
为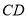 的中点,连接
的中点,连接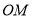 .
.
(1)求证: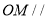 平面
平面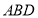 ;
;
(2)若 ,求三棱锥
,求三棱锥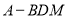 的体积.
的体积.
练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
题目内容
如图,在多面体 中,△
中,△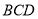 是等边三角形,△
是等边三角形,△ 是等腰直角三角形,
是等腰直角三角形,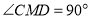 ,平面
,平面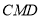 ⊥平面
⊥平面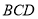 ,
,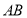 ⊥平面
⊥平面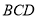 ,点
,点 为
为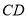 的中点,连接
的中点,连接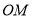 .
.

(1)求证: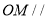 平面
平面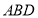 ;
;
(2)若 ,求三棱锥
,求三棱锥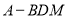 的体积.
的体积.
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案