题目内容
【题目】如图,多面体ABCDS中,面ABCD为矩形,SD⊥AD,且SD⊥AB,AD=1,AB=2,SD= ![]() .
. 
(1)求证:CD⊥平面ADS;
(2)求AD与SB所成角的余弦值;
(3)求二面角A﹣SB﹣D的余弦值.
【答案】
(1)证明:∵ABCD是矩形,∴CD⊥AD
又SD⊥AB,AB∥CD,则CD⊥SD
AD⊥SD
∴CD⊥平面ADS
(2)解:矩形ABCD,∴AD∥BC,即BC=1,
∴要求AD与SB所成的角,即求BC与SB所成的角
在△SBC中,由(1)知,SD⊥面ABCD.
∴Rt△SDC中, ![]()
∴CD是CS在面ABCD内的射影,且BC⊥CD,
∴SC⊥BC
tan∠SBC= ![]()
cos∠SBC= ![]()
从而SB与AD的成的角的余弦为 ![]()
(3)∵△SAD中SD⊥AD,且SD⊥AB
∴SD⊥面ABCD.
∴平面SDB⊥平面ABCD,BD为面SDB与面ABCD的交线.
∴过A作AE⊥DB于E∴AE⊥平面SDB
又过A作AF⊥SB于F,连接EF,
从而得:EF⊥SB
∴∠AFB为二面角A﹣SB﹣D的平面角
在矩形ABCD中,对角线∵ ![]()
BD= ![]() ∴在△ABD中,AE=
∴在△ABD中,AE= ![]()
由(2)知在Rt△SBC, ![]() .
.
而Rt△SAD中,SA=2,且AB=2,∴SB2=SA2+AB2,
∴△SAB为等腰直角三角形且∠SAB为直角,
∴ ![]()
∴ 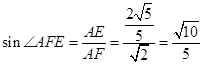
所以所求的二面角的余弦为 ![]()

【解析】(1)要证CD⊥平面ADS,只需证明直线CD垂直平面ADS内的两条相交直线AD、SD即可;(2)要求AD与SB所成的角,即求BC与SB所成的角,解三角形可求AD与SB所成角的余弦值;(3)过A作AE⊥DB于E 又过A作AF⊥SB于F,连接EF,说明∠AFB为二面角A﹣SB﹣D的平面角,解三角形可求二面角A﹣SB﹣D的余弦值.
【考点精析】掌握异面直线及其所成的角和直线与平面垂直的判定是解答本题的根本,需要知道异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】为了解高中生作文成绩与课外阅读量之间的关系,某研究机构随机抽取了60名高中生,通过问卷调查,得到以下数据:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

由以上数据,计算得到K2的观测值k≈9.643,根据临界值表,以下说法正确的是( )
A. 没有充足的理由认为课外阅读量大与作文成绩优秀有关
B. 有0.5%的把握认为课外阅读量大与作文成绩优秀有关
C. 有99.9%的把握认为课外阅读量大与作文成绩优秀有关
D. 有99.5%的把握认为课外阅读量大与作文成绩优秀有关
【题目】第31届夏季奥林匹克运动会于2016年8月5日至8月21日在巴西里约热内卢举行.如表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
第30届伦敦 | 第29届北京 | 第28届雅典 | 第27届悉尼 | 第26届亚特兰大 | |
中国 | 38 | 51 | 32 | 28 | 16 |
俄罗斯 | 24 | 23 | 27 | 32 | 26 |
(1)根据表格中两组数据在答题卡上完成近五届奥运会两国代表团获得的金牌数的茎叶图,并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度(不要求计算出具体数值,给出结论即可);
(2)如表是近五届奥运会中国代表团获得的金牌数之和![]() (从第26届算起,不包括之前已获得的金牌数)随时间
(从第26届算起,不包括之前已获得的金牌数)随时间![]() 变化的数据:
变化的数据:
时间 | 26 | 27 | 28 | 29 | 30 |
金牌数之和 | 16 | 44 | 76 | 127 | 165 |
作出散点图如图:

由图可以看出,金牌数之和![]() 与时间
与时间![]() 之间存在线性相关关系,请求出
之间存在线性相关关系,请求出![]() 关于
关于![]() 的线性回归方程,并预测到第32届奥运会时中国代表团获得的金牌数之和为多少?
的线性回归方程,并预测到第32届奥运会时中国代表团获得的金牌数之和为多少?

