题目内容
在△ABC中,已知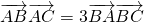 .
.
(1)求证:tanB=3tanA;
(2)若tanC=2,求A的值.
解:(1)因为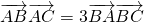 ,所以AB•AC•cosA=3BA•BC•cosB,…(2分)
,所以AB•AC•cosA=3BA•BC•cosB,…(2分)
即AC•cosA=3BC•cosB,由正弦定理知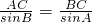
从而sinBcosA=3cosBsinA…(4分)
因为A、B∈(0,π),结合上式可得cosA,cosB同号,只能为正,
同除以cosAcosB可得tanB=3tanA…(6分)
(2)因为tanC=2,所以tan[π-(A+B)]=2即tan(A+B)=-2…(8分)
即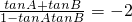 ,由(1)得
,由(1)得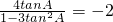
解得tanA=1或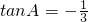 …(12分)
…(12分)
因为cosA>0,故tanA=1,所以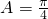 …(13分)
…(13分)
分析:(1)由题意可得AB•AC•cosA=3BA•BC•cosB,即AC•cosA=3BC•cosB,结合正弦定理可得sinBcosA=3cosBsinA,同除以cosAcosB可得答案;(2)由已知可得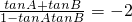 ,代入(1)得
,代入(1)得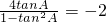 ,解得tanA=1或
,解得tanA=1或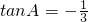 ,结合cosA>0,可得答案.
,结合cosA>0,可得答案.
点评:本题考查三角函数的运算,涉及向量的数量积,属中档题.
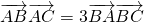 ,所以AB•AC•cosA=3BA•BC•cosB,…(2分)
,所以AB•AC•cosA=3BA•BC•cosB,…(2分)即AC•cosA=3BC•cosB,由正弦定理知
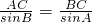
从而sinBcosA=3cosBsinA…(4分)
因为A、B∈(0,π),结合上式可得cosA,cosB同号,只能为正,
同除以cosAcosB可得tanB=3tanA…(6分)
(2)因为tanC=2,所以tan[π-(A+B)]=2即tan(A+B)=-2…(8分)
即
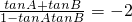 ,由(1)得
,由(1)得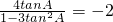
解得tanA=1或
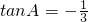 …(12分)
…(12分)因为cosA>0,故tanA=1,所以
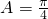 …(13分)
…(13分)分析:(1)由题意可得AB•AC•cosA=3BA•BC•cosB,即AC•cosA=3BC•cosB,结合正弦定理可得sinBcosA=3cosBsinA,同除以cosAcosB可得答案;(2)由已知可得
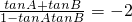 ,代入(1)得
,代入(1)得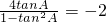 ,解得tanA=1或
,解得tanA=1或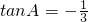 ,结合cosA>0,可得答案.
,结合cosA>0,可得答案.点评:本题考查三角函数的运算,涉及向量的数量积,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目