题目内容
已知函数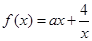 .
.
(1)从区间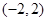 内任取一个实数
内任取一个实数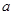 ,设事件
,设事件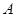 ={函数
={函数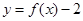 在区间
在区间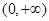 上有两个不同的零点},求事件
上有两个不同的零点},求事件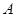 发生的概率;
发生的概率;
(2)若连续掷两次骰子(骰子六个面上标注的点数分别为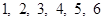 )得到的点数分别为
)得到的点数分别为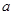 和
和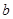 ,记事件
,记事件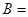 {
{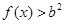 在
在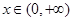 恒成立},求事件
恒成立},求事件 发生的概率.
发生的概率.
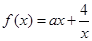 .
.(1)从区间
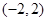 内任取一个实数
内任取一个实数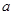 ,设事件
,设事件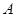 ={函数
={函数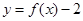 在区间
在区间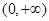 上有两个不同的零点},求事件
上有两个不同的零点},求事件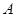 发生的概率;
发生的概率;(2)若连续掷两次骰子(骰子六个面上标注的点数分别为
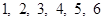 )得到的点数分别为
)得到的点数分别为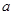 和
和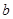 ,记事件
,记事件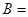 {
{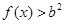 在
在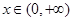 恒成立},求事件
恒成立},求事件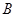 发生的概率.
发生的概率.(1)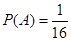 ;(2)
;(2)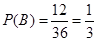 .
.
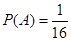 ;(2)
;(2)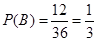 .
.试题分析:(1)根据函数
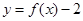 在区间
在区间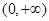 上有两个不同的零点,
上有两个不同的零点,得知
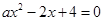 有两个不同的正根
有两个不同的正根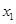 和
和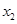 ,
,由不等式组
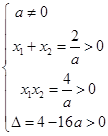
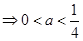 ,利用几何概型得解.
,利用几何概型得解.(2)应用基本不等式得到
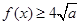 ,
,由于
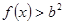 在
在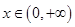 恒成立,得到
恒成立,得到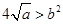 ;
;讨论当
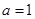 ,
,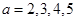 ,
,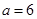 的情况,
的情况,得到满足条件的基本事件个数,而基本事件总数为
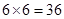 , 故应用古典概型概率的计算公式即得解.
, 故应用古典概型概率的计算公式即得解.试题解析:(1)
 函数
函数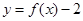 在区间
在区间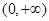 上有两个不同的零点,
上有两个不同的零点,
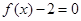 ,即
,即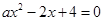 有两个不同的正根
有两个不同的正根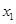 和
和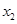
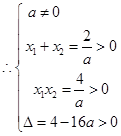
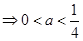 4分
4分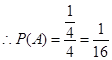 6分
6分(2)由已知:
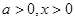 ,所以
,所以 ,即
,即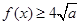
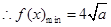 ,
, 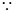
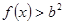 在
在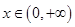 恒成立
恒成立 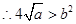
 8分
8分当
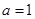 时,
时, 适合
适合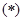 ;
; 当
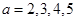 时,
时, 均适合
均适合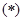 ;
; 当
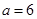 时,
时,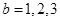 均适合
均适合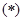 ;
; 满足
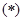 的基本事件个数为
的基本事件个数为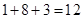 . 10分
. 10分而基本事件总数为
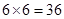 , 11分
, 11分 . 12分
. 12分 
练习册系列答案
相关题目

 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原 个元件,寿命为
个元件,寿命为 之间的应抽取几个;
之间的应抽取几个; 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为 ,一个寿命为
,一个寿命为 ”的概率.
”的概率.



 )分成六段
)分成六段 ,
, ,
, ,
, ,
, ,
, 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图. ,
, , ,
, , (
( 为车速在
为车速在 ,
, , ,
, , (
( 为车速在
为车速在 的车辆中任意抽取
的车辆中任意抽取 辆共有几种情况?请列举出所有的情况,并求抽取的
辆共有几种情况?请列举出所有的情况,并求抽取的
 ,(i=1,2,3,4).
,(i=1,2,3,4). ;
; 的是( )
的是( )