题目内容
数列 满足
满足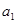 ,
,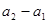 ,
, ,…,
,…,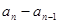 是首项为
是首项为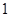 ,公比为
,公比为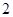 的等比数列,那么
的等比数列,那么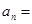 ( )
( )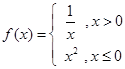
A.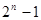 | B.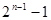  | C.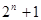 | D.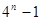 |
A
解析试题分析:因为an是等比数列{an-an-1}的前n项和,利用等比数列的前n项公式可得an,那么可知an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=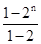 =
=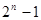 ,故选A.
,故选A.
考点:本试题主要考查了等比数列的通项公式的运用。
点评:解决该试题的关键是在于观察出所给等比数列,与an有什么关系,观察出来,此题迎刃而解.体现了累加法的求和的运用。

练习册系列答案
相关题目
设 成等比数列,其公比为2,则
成等比数列,其公比为2,则 的值为( )
的值为( )
A. | B. | C. | D.1 |
已知等比数列 中,各项都是正数,且3
中,各项都是正数,且3 ,
, 成等差数列,则
成等差数列,则
| A.1 | B. | C.3 | D. |
已知各项均为正数的等比数列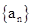 中,
中,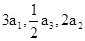 成等差数列,则
成等差数列,则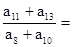 ( )
( )
A. 或3 或3 | B.3 | C.27 | D.1或27 |
等比数列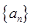 中,
中,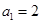 ,
, =4,函数
=4,函数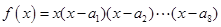 ,则
,则 ( )
( )
A.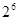 | B.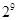 | C.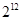 | D. |
某工厂2009年生产某种产品2万件,计划从2010年起每年比上一年增长20%,这个工厂年产量超过12万的最早的一年是(注:lg2=0.3010,lg3=0.4771)
| A.2018年 | B.2019年 | C.2020年 | D.2021年 |
已知各项均为正数的等比数列{ },
},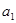 ·
· =16,则
=16,则 ·
·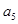 ·
· 的值( )
的值( )
| A.16 | B.32 | C.48 | D.64 |
设{an}是有正数组成的等比数列,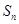 为其前n项和。已知a2a4="1,"
为其前n项和。已知a2a4="1," 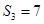 ,则
,则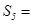
A. | B. | C.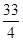 | D.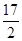 |
设{an}是有正数组成的等比数列, 为其前n项和。已知a2a4="1,"
为其前n项和。已知a2a4="1," 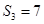 ,则
,则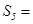 ( )
( )
A.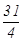 | B. | C. | D.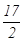 |