题目内容
已知各项均为正数的等比数列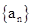 中,
中,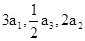 成等差数列,则
成等差数列,则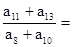 ( )
( )
A. 或3 或3 | B.3 | C.27 | D.1或27 |
C
解析试题分析:因为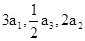 成等差数列,所以
成等差数列,所以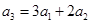 ,设公比为
,设公比为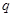 ,所以
,所以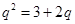 ,解得
,解得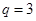 或
或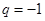 (舍),所以
(舍),所以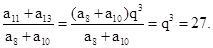
考点:本小题主要考查等差数列和等比数列中的基本运算,考查学生的运算求解能力.
点评:求出公比后,看出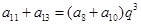 是简化此解题过程的关键.
是简化此解题过程的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
在等比数列{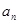 }中,若
}中,若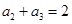 ,
,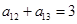 ,则
,则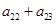 的值是( )
的值是( )
A.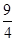 | B.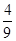 | C.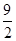 | D.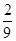 |
已知数列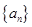 是各项均为正数且公比不等于
是各项均为正数且公比不等于 的等比数列.对于函数
的等比数列.对于函数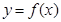 ,若数列
,若数列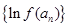 为等差数列,则称函数
为等差数列,则称函数 为“保比差数列函数”.现有定义在
为“保比差数列函数”.现有定义在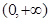 上的如下函数:①
上的如下函数:①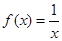 , ②
, ②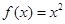 , ③
, ③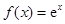 , ④
, ④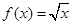 ,
,
则为“保比差数列函数”的所有序号为( )
| A.①② | B.③④ | C.①②④ | D.②③④ |
设 为等比数列
为等比数列 的前
的前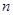 项和,已知
项和,已知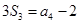 ,
,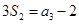 ,则公比
,则公比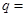 ( )
( )
| A.3 | B.4 | C.5 | D.6 |
已知等比数列 中,有
中,有 ,数列
,数列 是等差数列,且
是等差数列,且 ,则
,则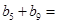 ( )
( )
| A.2 | B.4 | C.8 | D.16 |
在等比数列 中,
中, ,则数列
,则数列 的第4项为
的第4项为
A.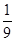 | B.81 | C.-81 | D.81或-81 |
数列 满足
满足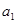 ,
,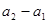 ,
, ,…,
,…,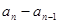 是首项为
是首项为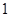 ,公比为
,公比为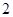 的等比数列,那么
的等比数列,那么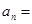 ( )
( )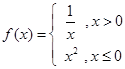
A.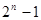 | B.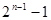  | C.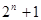 | D.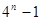 |
已知等比数列 中,
中, ,则其前3项的和
,则其前3项的和 的取值范围是
的取值范围是
A. | B.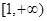 |
C.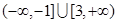 | D.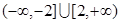 |
设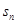 为等比数列
为等比数列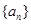 的前n项和,
的前n项和, 则
则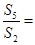
 ( )
( )
| A.-11 | B.-8 | C.5 | D.11 |