题目内容
下列命题中:(1)若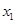 满足
满足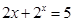 ,
,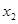 满足
满足 ,则
,则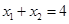 ;
;
(2)函数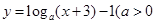 且
且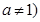 的图象恒过定点A,若A在
的图象恒过定点A,若A在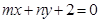 上,其中
上,其中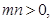 则
则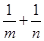 的最小值是
的最小值是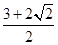 ; (3)设
; (3)设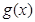 是定义在R上,以1为周期的函数,若
是定义在R上,以1为周期的函数,若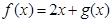 在
在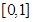 上的值域为
上的值域为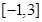 ,则
,则 在区间
在区间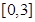 上的值域为
上的值域为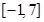 ; (4)已知曲线
; (4)已知曲线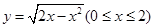 与直线
与直线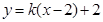 仅有2个交点,则
仅有2个交点,则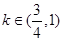 ; (5)函数
; (5)函数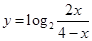 图象的对称中心为(2,1)。
图象的对称中心为(2,1)。
其中真命题序号为 .
(2)(3)(5)
解析试题分析:
(1) 若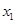 满足
满足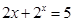 ,则
,则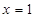 时,代入左边有
时,代入左边有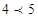 ,当
,当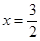 时,代入左边有
时,代入左边有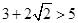 ,所以此时方程中
,所以此时方程中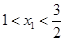 ;
;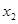 满足
满足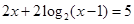 ,则
,则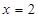 时代入左边有
时代入左边有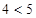 ,当
,当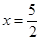 时代入左边有
时代入左边有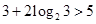 ,所以此时方程中
,所以此时方程中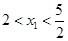 .
.
所以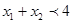 ,错误.
,错误.
(2)函数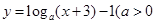 且
且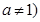 的图像恒过定点
的图像恒过定点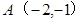 ,因为
,因为 在直线
在直线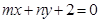 上,代入有
上,代入有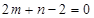 ,可得
,可得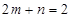 .则
.则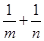
 ,因为
,因为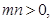 所以
所以 ,根据均值不等式可知
,根据均值不等式可知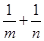
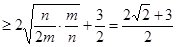 ,当且仅当
,当且仅当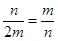 ,即
,即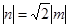 时取得等号.正确.
时取得等号.正确.
(3) 因为函数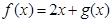 在
在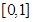 上的值域为
上的值域为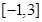 ,设
,设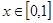 ,则
,则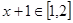 ,所以
,所以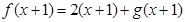 ,因为
,因为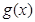 是定义在R上,以1为周期的函数,所以
是定义在R上,以1为周期的函数,所以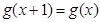 ,则有
,则有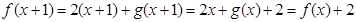 ,所以此时令
,所以此时令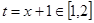 ,则函数
,则函数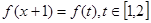 的值域是在
的值域是在 值域基础上上移2个单位得到的为
值域基础上上移2个单位得到的为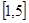 ;同理可设
;同理可设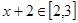 ,通过寻找
,通过寻找 值域关系可得
值域关系可得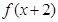 的值域为
的值域为 .综上可知
.综上可知 在
在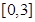 上的值域为
上的值域为 .正确;
.正确;
(4) 根据曲线方程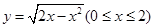 知
知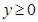 ,可化简为
,可化简为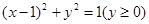 ,表示以
,表示以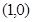 为圆心,1为半径的圆的
为圆心,1为半径的圆的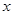 轴及其以上部分的曲线.直线
轴及其以上部分的曲线.直线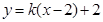 表示经过定点
表示经过定点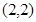 有斜率的直线.因为两者有两个交点,所以画图可知,当直线与曲线相切时,
有斜率的直线.因为两者有两个交点,所以画图可知,当直线与曲线相切时,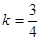 ,当恰有两个交点时,直线过原点,所以
,当恰有两个交点时,直线过原点,所以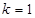 ,综上可知
,综上可知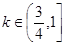 ,错误.
,错误.
(5) 函数的定义域为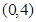 .
.
如果函数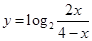 图象的对称中心为
图象的对称中心为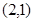 ,那么函数上的点
,那么函数上的点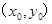 关于
关于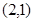 的对称点
的对称点 也在函数上.
也在函数上.
所以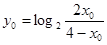 根据对数的运算法则可得
根据对数的运算法则可得
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 的定义域为 .
的定义域为 .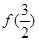 =
= 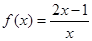 的反函数是
的反函数是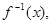 则
则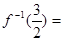 。
。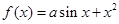 ,若
,若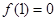 ,则
,则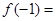 .
.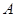 表示值域为R的函数组成的集合,
表示值域为R的函数组成的集合, 表示具有如下性质的函数
表示具有如下性质的函数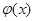 组成的集合:对于函数
组成的集合:对于函数 ,使得函数
,使得函数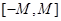 。例如,当
。例如,当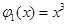 ,
,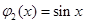 时,
时, ,
,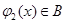 .现有如下命题:
.现有如下命题: 的定义域为
的定义域为 ,则“
,则“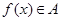 ”的充要条件是“
”的充要条件是“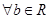 ,
,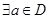 ,
, ”;
”;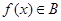 ,则
,则 的定义域相同,且
的定义域相同,且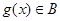 ,则
,则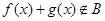 ;
;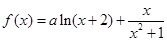 (
(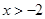 ,
,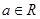 )有最大值,则
)有最大值,则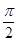 )上不是凸函数的是________.
)上不是凸函数的是________.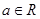 ,函数
,函数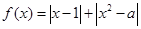 ,若
,若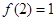 ,则
,则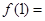 .
. (x+|x|),则函数f[f(x)]的值域为________.
(x+|x|),则函数f[f(x)]的值域为________.