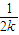题目内容
在用数学归纳法证明f（n）=
+
+…+
＜1（n∈N*，n≥3）的过程中：假设当n=k（k∈N*，k≥3）时，不等式f（k）＜1成立，则需证当n=k+1时，f（k+1）＜1也成立．若f（k+1）=f（k）+g（k），则g（k）=（ ）
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2n |
A．
| B．
| ||||||||||
C．
| D．
|
∵f（k）=
+
+…+
，f（k+1）=
+
+…+
+
+
∴f（k+1）-f（k）=
+
-
∵f（k+1）=f（k）+g（k），
∴g（k）=
+
-
故选B．
| 1 |
| k |
| 1 |
| k+1 |
| 1 |
| 2k |
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
∴f（k+1）-f（k）=
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
| 1 |
| k |
∵f（k+1）=f（k）+g（k），
∴g（k）=
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
| 1 |
| k |
故选B．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
+
+…+
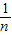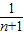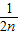＜1（n∈N*，n≥3）的过程中：假设当n=k（k∈N*，k≥3）时，不等式f（k）＜1成立，则需证当n=k+1时，f（k+1）＜1也成立．若f（k+1）=f（k）+g（k），则g（k）=（ ）
+
+
-
-
-
+
+…+
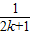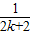
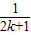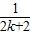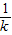
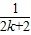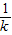
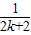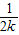
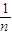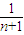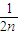＜1（n∈N*，n≥3）的过程中：假设当n=k（k∈N*，k≥3）时，不等式f（k）＜1成立，则需证当n=k+1时，f（k+1）＜1也成立．若f（k+1）=f（k）+g（k），则g（k）=（ ）
+
+
-
-
-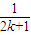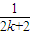
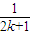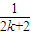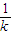
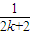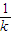
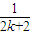