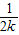题目内容
在用数学归纳法证明f（n）=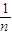
+
+…+
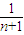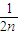＜1（n∈N*，n≥3）的过程中：假设当n=k（k∈N*，k≥3）时，不等式f（k）＜1成立，则需证当n=k+1时，f（k+1）＜1也成立．若f（k+1）=f（k）+g（k），则g（k）=（ ）A．
+
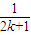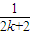
B．
+
-
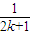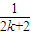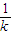
C．
-
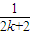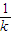
D．
-
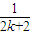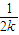
【答案】分析：根据f（n）=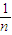
+
+…+
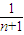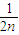，可知f（k）=
+…+
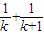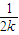，f（k+1）=
+…+
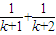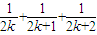，从而可得n=k到n=k+1变化了的项．
解答：解：∵f（k）=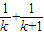
+…+
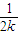，f（k+1）=
+…+
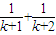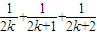
∴f（k+1）-f（k）=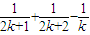
∵f（k+1）=f（k）+g（k），
∴g（k）=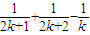
故选B．
点评：本题考查数学归纳法，考查数学归纳法中的推理，确定n=k到n=k+1变化了的项是解题的关键．
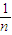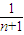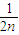++…+，可知f（k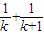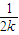）=+…+，f（k+1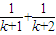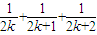）=+…+，从而可得n=k到n=k+1变化了的项．解答：解：∵f（k）=
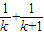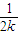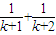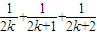
+…+，f（k+1）=+…+∴f（k+1）-f（k）=
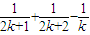
∵f（k+1）=f（k）+g（k），
∴g（k）=
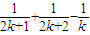
故选B．
点评：本题考查数学归纳法，考查数学归纳法中的推理，确定n=k到n=k+1变化了的项是解题的关键．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
+
+…+
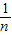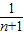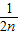＜1（n∈N*，n≥3）的过程中：假设当n=k（k∈N*，k≥3）时，不等式f（k）＜1成立，则需证当n=k+1时，f（k+1）＜1也成立．若f（k+1）=f（k）+g（k），则g（k）=（ ）
+
+
-
-
-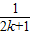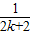
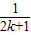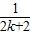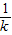
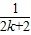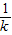
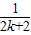