题目内容
在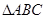 中,角
中,角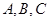 的对边分别是
的对边分别是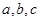 ,且
,且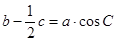
(Ⅰ)求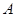 的值;
的值;
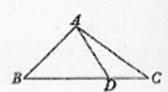
(Ⅱ)设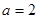 ,求
,求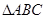 的面积的最大值
的面积的最大值
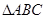 中,角
中,角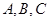 的对边分别是
的对边分别是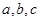 ,且
,且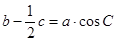
(Ⅰ)求
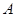 的值;
的值;(Ⅱ)设
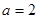 ,求
,求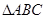 的面积的最大值
的面积的最大值(Ⅰ)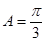 (Ⅱ)
(Ⅱ)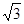
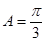 (Ⅱ)
(Ⅱ)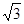
本试题主要是考查了解三角形的知识的运用。
(1)利用正弦定理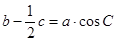 ,化边为角,得到
,化边为角,得到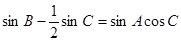 ,从而化简得到角A的值。
,从而化简得到角A的值。
(2)由余弦定理得
当且仅当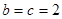 时,
时,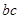 有最大值4
有最大值4
解:(1)由正弦定理得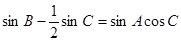 即
即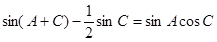
\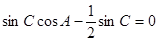 ,由于
,由于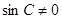 ,则
,则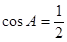 ,而
,而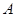 为内角,\
为内角,\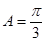
(2)由余弦定理得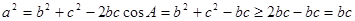
当且仅当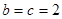 时,
时,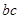 有最大值4
有最大值4
\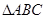 的面积的最大值
的面积的最大值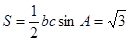
方法二:由正弦定理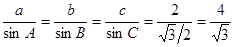
\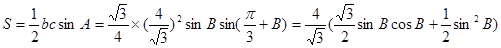
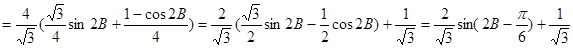 当
当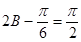 即
即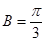 时,
时,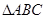 的面积有最大值
的面积有最大值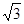
(1)利用正弦定理
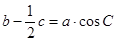 ,化边为角,得到
,化边为角,得到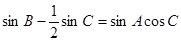 ,从而化简得到角A的值。
,从而化简得到角A的值。(2)由余弦定理得

当且仅当
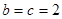 时,
时,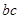 有最大值4
有最大值4解:(1)由正弦定理得
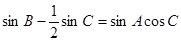 即
即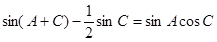
\
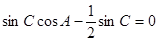 ,由于
,由于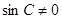 ,则
,则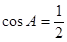 ,而
,而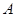 为内角,\
为内角,\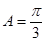
(2)由余弦定理得
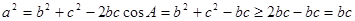
当且仅当
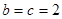 时,
时,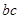 有最大值4
有最大值4\
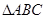 的面积的最大值
的面积的最大值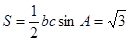
方法二:由正弦定理
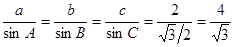
\
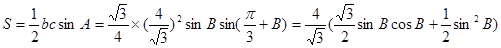
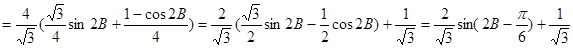 当
当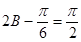 即
即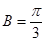 时,
时,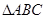 的面积有最大值
的面积有最大值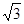

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 中,
中, .
. 的值; (2)若
的值; (2)若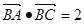 ,
, ,求
,求 和
和 的值。
的值。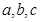 为
为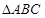 的三个内角
的三个内角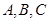 的对边,
的对边,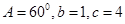 ,则
,则
 向分布于一条笔直公路旁的三个缺水村庄
向分布于一条笔直公路旁的三个缺水村庄 供水,已修建好了连接
供水,已修建好了连接 和
和 的输水管道,但由于
的输水管道,但由于 无法直接测量,所以先得预算,现已有以下数据:
无法直接测量,所以先得预算,现已有以下数据: ,
, 千米,
千米, 千米,
千米, ,试据以上条件预算
,试据以上条件预算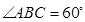 ,
,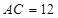 ,
,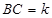 的
的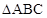 恰有一个,那么
恰有一个,那么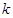 的取值范围是( )
的取值范围是( )
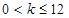
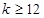
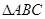 中,角
中,角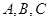 所对的边分别为
所对的边分别为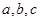 ,且满足
,且满足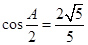 ,
,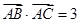 .
.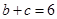 ,求
,求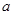 的值.
的值. ABC中, a,b,c分别是三个内角A,B,C的对边,若
ABC中, a,b,c分别是三个内角A,B,C的对边,若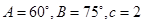 ,则
,则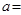 ___________.
___________. 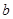 =2
=2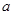 sin B,则角A为( )
sin B,则角A为( )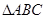 中,已知
中,已知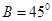 ,
,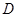 是
是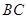 边上的一点,
边上的一点, 
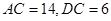 ,则
,则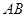 的长为 .
的长为 .