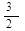题目内容
设向量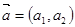 ,
,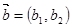 ,定义一种向量积
,定义一种向量积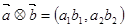 ,已知
,已知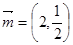 ,
,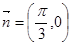 ,点
,点
 在
在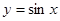 的图像上运动。
的图像上运动。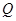 是函数
是函数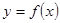 图像上的点,且满足
图像上的点,且满足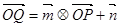 (其中O为坐标原点),则函数
(其中O为坐标原点),则函数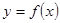 的值域是
的值域是
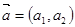 ,
,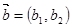 ,定义一种向量积
,定义一种向量积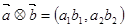 ,已知
,已知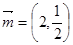 ,
,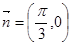 ,点
,点
 在
在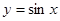 的图像上运动。
的图像上运动。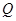 是函数
是函数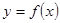 图像上的点,且满足
图像上的点,且满足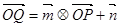 (其中O为坐标原点),则函数
(其中O为坐标原点),则函数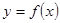 的值域是
的值域是 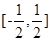
试题分析:设P
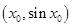 ,Q
,Q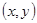 ,由题意易知:
,由题意易知: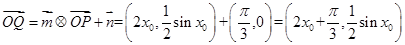 ,所以
,所以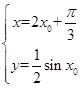 ,即点Q的轨迹方程为
,即点Q的轨迹方程为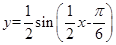 ,所以函数
,所以函数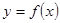 的值域是
的值域是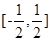 。
。 的值域;轨迹方程的求法。
的值域;轨迹方程的求法。点评:本题是创新题型,给出新定义,让我们直接根据新定义来做题,考查了我们的理解能力。本题实质上考查的是轨迹方程的求法。求曲线的轨迹方程是解析几何的基本问题之一。本题主要考查利用“相关点法”求曲线的轨迹方程。相关点法:用动点Q的坐标x,y表示相关点P的坐标x0、y0,然后代入点P的坐标(x0,y0)所满足的曲线方程,整理化简便得到动点Q轨迹方程,这种求轨迹方程的方法叫做相关点法.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
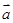 |=2,|
|=2,|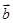 |=1,
|=1,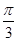 ,则向量2
,则向量2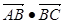 的值等于 .
的值等于 .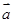 |=2|
|=2|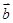 |≠0,且关于x的方程x2+|
|≠0,且关于x的方程x2+|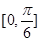
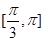
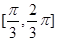
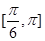
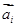 满足
满足 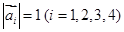 且
且 ,则
,则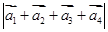 的最大值为 .
的最大值为 .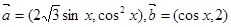 ,函数
,函数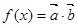
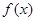 的单调递减区间.
的单调递减区间.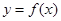 的图象向左平移
的图象向左平移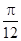 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的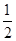 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数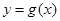 的图象.求
的图象.求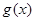 在
在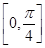
 上的值域.
上的值域.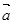 =(cos
=(cos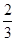
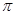 , sin
, sin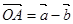 ,
, 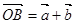 ,若△OAB是以O为直角顶点的等腰直角三角形,则△OAB的面积等于( )
,若△OAB是以O为直角顶点的等腰直角三角形,则△OAB的面积等于( )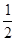
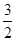
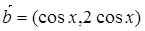
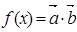 并求
并求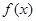 的单调递增区间。
的单调递增区间。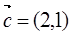 ,且
,且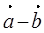 与
与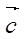 共线,
共线,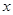 为第二象限角,求
为第二象限角,求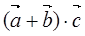 的值。
的值。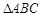 平面内一点
平面内一点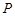 满足
满足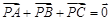 ,若实数
,若实数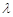 满足:
满足: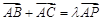 ,则
,则