题目内容
(本小题满分12分)
已知函数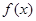 定义域为
定义域为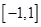 ,若对于任意的
,若对于任意的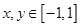 ,都有
,都有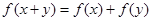 ,且
,且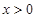 时,有
时,有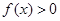 .
.
(1)求证: 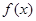 为奇函数;
为奇函数;
(2)求证: 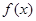 在
在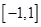 上为单调递增函数;
上为单调递增函数;
(3)设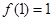 ,若
,若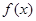 <
<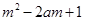 ,对所有
,对所有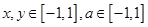 恒成立,求实数
恒成立,求实数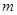 的取值范围.
的取值范围.
【答案】
(1)见解析(2)见解析(3)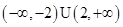
【解析】
试题分析:(1)因为有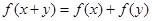 ,
,
令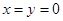 ,得
,得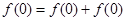 ,所以
,所以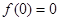 ,
……1分
,
……1分
令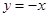 可得:
可得: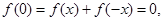
所以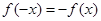 ,所以
,所以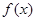 为奇函数.
……4分
为奇函数.
……4分
(2)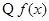 是定义在
是定义在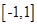 上的奇函数,由题意
上的奇函数,由题意
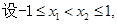 则
则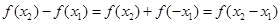 ,
,
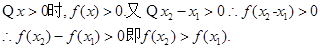
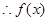 是在
是在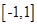 上为单调递增函数;
……8分
上为单调递增函数;
……8分
(3)因为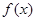 在
在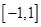 上为单调递增函数,
上为单调递增函数,
所以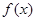 在
在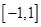 上的最大值为
上的最大值为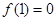 ,
……9分
,
……9分
所以要使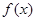 <
<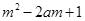 ,对所有
,对所有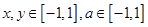 恒成立,
恒成立,
只要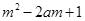 >1,即
>1,即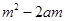 >0,
……10分
>0,
……10分
令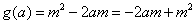
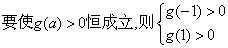
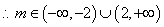 .
……12分
.
……12分
考点:本小题主要考查有关抽象函数的奇偶性、单调性和恒成立问题,考查学生分析问题、解决问题和灵活转化的能力.
点评:解决抽象函数问题常用的方法是“赋值法”,而要考查抽象函数的性质,还要借助图象,数形结合来解决.对于恒成立问题,要转为为求最值来解决,而(3)中将函数转化为关于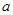 的函数,是这道题解题的亮点所在.
的函数,是这道题解题的亮点所在.

练习册系列答案
相关题目