题目内容
已知x，y∈R．（I）若x＞0，y＞0且
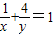，求x+y的最小值；（II）若
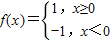，求不等式x+（x+2）•f（x+2）≤5的解集．
【答案】分析：（I）利用“1”的代换，结合基本不等式，即可求出x+y的最小值；
（II）确定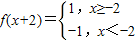
，再分类讨论，即可得到结论．
解答：解：（I）因为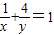
，所以
又因为x＞0，y＞0，所以
当且仅当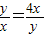
，即y=2x，即x=3，y=6时，等号成立
所以当x=3，y=6时，x+y取最小值9（5分）
（II）因为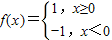
，所以
当x≥-2时，不等式x+（x+2）•f（x+2）≤5转化为x+（x+2）•1≤5解得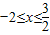
当x＜-2时，不等式x+（x+2）•f（x+2）≤5转化为x+（x+2）•（-1）≤5解得x＜-2
综上不等式x+（x+2）•f（x+2）≤5的解集为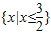
（11分）
点评：本题考查基本不等式的运用，考查不等式的解法，考查学生的计算能力，属于中档题．
（II）确定
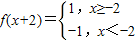，再分类讨论，即可得到结论．解答：解：（I）因为
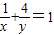，所以又因为x＞0，y＞0，所以
当且仅当
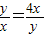，即y=2x，即x=3，y=6时，等号成立所以当x=3，y=6时，x+y取最小值9（5分）
（II）因为
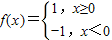，所以当x≥-2时，不等式x+（x+2）•f（x+2）≤5转化为x+（x+2）•1≤5解得
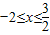
当x＜-2时，不等式x+（x+2）•f（x+2）≤5转化为x+（x+2）•（-1）≤5解得x＜-2
综上不等式x+（x+2）•f（x+2）≤5的解集为
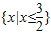（11分）点评：本题考查基本不等式的运用，考查不等式的解法，考查学生的计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目