题目内容
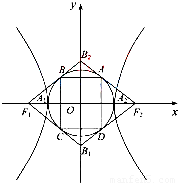
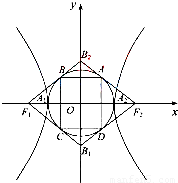
如图，双曲线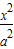
-
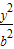=1（a，b＞0）的两顶点为A1，A2，虚轴两端点为B1，B2，两焦点为F1，F2．若以A1A2为直径的圆内切于菱形F1B1F2B2，切点分别为A，B，C，D．则：（Ⅰ）双曲线的离心率e= ；
（Ⅱ）菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值
= ．
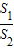【答案】分析：（Ⅰ）直线B2F1的方程为bx-cy+bc=0，所以O到直线的距离为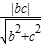
，根据以A1A2为直径的圆内切于菱形F1B1F2B2，可得
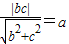，由此可求双曲线的离心率；
（Ⅱ）菱形F1B1F2B2的面积S1=2bc，求出矩形ABCD的长与宽，从而求出面积S2=4mn=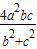
，由此可得结论．
解答：解：（Ⅰ）直线B2F1的方程为bx-cy+bc=0，所以O到直线的距离为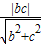
∵以A1A2为直径的圆内切于菱形F1B1F2B2，
∴
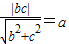
∴（c2-a2）c2=（2c2-a2）a2
∴c4-3a2c2+a4=0
∴e4-3e2+1=0
∵e＞1
∴e=
（Ⅱ）菱形F1B1F2B2的面积S1=2bc
设矩形ABCD，BC=2m，BA=2n，∴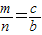
∵m2+n2=a2，∴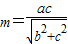
，
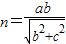
∴面积S2=4mn=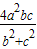
∴
=
=
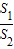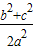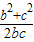
∵bc=a2=c2-b2
∴
∴
=
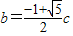
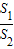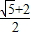
故答案为：
，
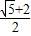
点评：本题考查圆与圆锥曲线的综合，考查双曲线的性质，面积的计算，解题的关键是确定几何量之间的关系．
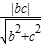，根据以A1A2为直径的圆内切于菱形F1B1F2B2，可得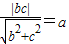，由此可求双曲线的离心率；（Ⅱ）菱形F1B1F2B2的面积S1=2bc，求出矩形ABCD的长与宽，从而求出面积S2=4mn=
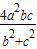，由此可得结论．解答：解：（Ⅰ）直线B2F1的方程为bx-cy+bc=0，所以O到直线的距离为
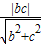
∵以A1A2为直径的圆内切于菱形F1B1F2B2，
∴
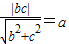
∴（c2-a2）c2=（2c2-a2）a2
∴c4-3a2c2+a4=0
∴e4-3e2+1=0
∵e＞1
∴e=
（Ⅱ）菱形F1B1F2B2的面积S1=2bc
设矩形ABCD，BC=2m，BA=2n，∴
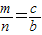
∵m2+n2=a2，∴
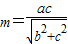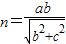
，∴面积S2=4mn=
∴
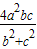
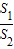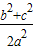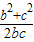
==∵bc=a2=c2-b2
∴
∴
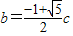
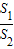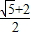
=故答案为：
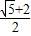
，点评：本题考查圆与圆锥曲线的综合，考查双曲线的性质，面积的计算，解题的关键是确定几何量之间的关系．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
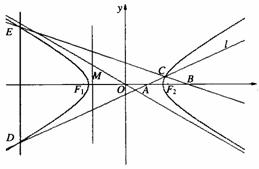
=1（a＞0，b＞0）的离心率为
，F1、F2分别为左、右焦点， 
.
，0)（0＜m＜1）是x轴上的两点．过点A作斜率不为0的直线l，使得l交双曲线于C、D两点，作直线BC交双曲线于另一点E．证明直线DE垂直于x轴．
=1(b∈N*)的两个焦点为F1、F2，P为双曲线上一点，|OP|＜5,|PF1|、|F1F2|、|PF2|成等差数列，求此双曲线方程.
=1（a＞0，b＞0）的离心率为
、F2分别为左、右焦点，M为左准线与渐近线在第二象限内的交点，且
．
（0＜m＜1）是x轴上的两点．过点A作斜率不为0的直线l，使得l交双曲线于C、D两点，作直线BC交双曲线于另一点E．证明直线DE垂直于x轴．中心O为圆心，分别以a和b为半径作大圆和．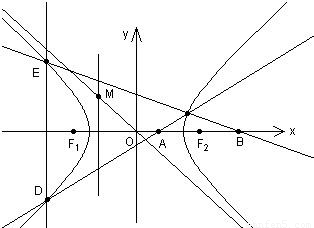
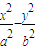=1（a＞0，b＞0）的离心率为
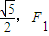、F2分别为左、右焦点，M为左准线与渐近线在第二象限内的交点，且
．
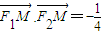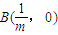（0＜m＜1）是x轴上的两点．过点A作斜率不为0的直线l，使得l交双曲线于C、D两点，作直线BC交双曲线于另一点E．证明直线DE垂直于x轴．中心O为圆心，分别以a和b为半径作大圆和．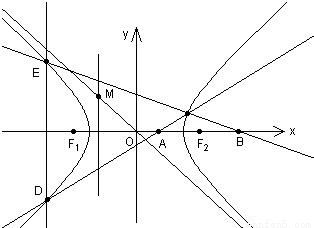
-
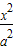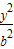=1（a，b＞0）的两顶点为A1，A2，虚轴两端点为B1，B2，两焦点为F1，F2．若以A1A2为直径的圆内切于菱形F1B1F2B2，切点分别为A，B，C，D．则：
= ．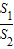