题目内容
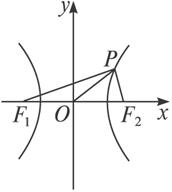
如图，双曲线
=1(b∈N*)的两个焦点为F1、F2，P为双曲线上一点，|OP|＜5,|PF1|、|F1F2|、|PF2|成等差数列，求此双曲线方程.
双曲线方程为
-y2=1.
解析:
∵|PF1|、|F1F2|、|PF2|成等差数列，
∴|PF1|+|PF2|=2|F1F2|=4c.
又|PF1|-|PF2|=2a=4,
∴|PF1|=2c+2,|PF2|=2c-2.
根据中线定理有|PF1|2+|PF2|2=2(|PO|2+|F1O|2)＜2(52+c2),
∴(2c+2)2+(2c-2)2＜2(52+c2).
∴8c2+8＜50+2c2.∴c2＜7,
即4+b2＜7.∴b2＜3.
又b∈N*,∴b=1.
∴所求双曲线方程为-y2=1.
练习册系列答案
相关题目
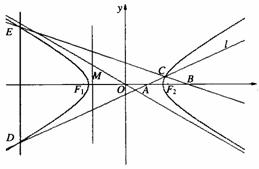
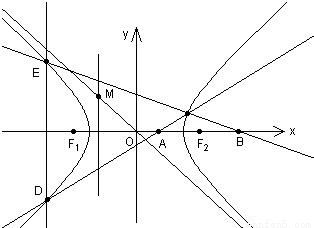
=1（a＞0，b＞0）的离心率为
，F1、F2分别为左、右焦点， 
.
，0)（0＜m＜1）是x轴上的两点．过点A作斜率不为0的直线l，使得l交双曲线于C、D两点，作直线BC交双曲线于另一点E．证明直线DE垂直于x轴．
=1（a＞0，b＞0）的离心率为
、F2分别为左、右焦点，M为左准线与渐近线在第二象限内的交点，且
．
（0＜m＜1）是x轴上的两点．过点A作斜率不为0的直线l，使得l交双曲线于C、D两点，作直线BC交双曲线于另一点E．证明直线DE垂直于x轴．中心O为圆心，分别以a和b为半径作大圆和．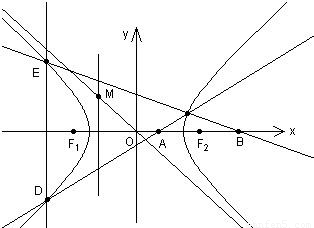
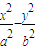=1（a＞0，b＞0）的离心率为
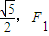、F2分别为左、右焦点，M为左准线与渐近线在第二象限内的交点，且
．
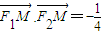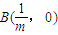（0＜m＜1）是x轴上的两点．过点A作斜率不为0的直线l，使得l交双曲线于C、D两点，作直线BC交双曲线于另一点E．证明直线DE垂直于x轴．中心O为圆心，分别以a和b为半径作大圆和．
=1(b∈N*)的两个焦点为F1、F2，P为双曲线上一点，|OP|＜5,|PF1|、|F1F2|、|PF2|成等差数列，求此双曲线方程.