题目内容
已知函数![]() ,在(-∞,-1),(2,+∞)上单调递增,在(-1,2)上单调递减,当且仅当x>4时,
,在(-∞,-1),(2,+∞)上单调递增,在(-1,2)上单调递减,当且仅当x>4时,![]() .
.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若函数![]() 与函数f(x)、g(x)的图象共有3个交点,求m的取值范围.
与函数f(x)、g(x)的图象共有3个交点,求m的取值范围.
(I)f(x)= x3-![]() x2-6x-11
x2-6x-11
(II)m的取值范围是(-21,-![]() )∪(1,5)∪(5,+∞)
)∪(1,5)∪(5,+∞)
解析:
(I)f(x)=3x2+2ax+b,由题意,-1,2是方程f’(x)=0的两根.
∴ 4分
4分
∴f(x1)=x3-![]() x2-6x+0
x2-6x+0
令h(x)=f(x)-g(x)= x3-![]() x2-2x+c-5
x2-2x+c-5
h’(x)=3x2-5x-2=(3x+1) (x-2)
当x>4时,h’(x)>0,h(x)是增函数,∴h(4)=11+c=0 ∴c=-11 7分
∴f(x)= x3-![]() x2-6x-11 8分
x2-6x-11 8分
(Ⅱ)g(x)=(x-2)2+1 当x=2时,g(x)min=1
f(x)极大值=f(-1)=-![]() f(x)极小值=f(2)=-2l 11分
f(x)极小值=f(2)=-2l 11分
作出函数f(x)、g(x)的草图,由图可得,当函数y=m与函数f(x)、g(x)的图象共有3个交点,
m的取值范围是(-21,-![]() )∪(1,5)∪(5,+∞) 15分
)∪(1,5)∪(5,+∞) 15分

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
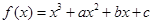 ,曲线
,曲线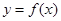 在点
在点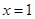 处的切线为
处的切线为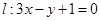 ,若
,若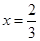 时,
时, 的值;
的值;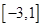 上的最大值和最小值.
上的最大值和最小值. 定义在区间
定义在区间 上,
上, ,且当
,且当 时,
时, .又数列
.又数列 满足
满足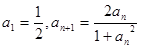 .
. 的表达式;
的表达式; 为数列
为数列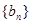 的前
的前 项和,若
项和,若 对
对 恒成立,求
恒成立,求 的最小值.
的最小值. 和
和 在
在 的图象如下图表示:
的图象如下图表示:
 有且仅有6个根; ②方程
有且仅有6个根; ②方程 有且仅有3个根;
有且仅有3个根; 有且仅有5个根; ④方程
有且仅有5个根; ④方程 有且仅有4个根;
有且仅有4个根;