题目内容
已知函数 定义在区间
定义在区间 上,
上, ,且当
,且当 时,
时,
恒有 .又数列
.又数列 满足
满足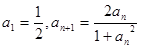 .
.
(1)证明: 在
在 上是奇函数;
上是奇函数;
(2)求 的表达式;
的表达式;
(3)设 为数列
为数列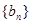 的前
的前 项和,若
项和,若 对
对 恒成立,求
恒成立,求 的最小值.
的最小值.
【答案】
(Ⅰ)证明略
(Ⅱ) 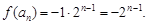
(III) m的最小值为7.
【解析】本试题主要是考查了函数与数列的综合运用
(1)通过赋值法得到函数奇偶性的判定。
(2)因为令x=an,y=-an,于是,由已知得2f (an)=f (an+1),从而求解得到解析式。
(3)由(II)得f(an+1)=-2n,那么整体思想得到参数m的最值。

练习册系列答案
相关题目
 定义在区间
定义在区间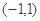 上,
上,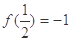 ,且当
,且当 时,恒有
时,恒有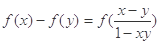 .又数列
.又数列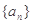 满足
满足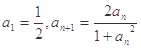 .
.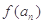 的表达式;
的表达式;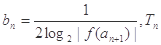 为数列
为数列 的前
的前 项和,若
项和,若 对
对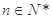 恒成立,求
恒成立,求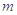 的最小值.
的最小值.