题目内容
已知函数定义在R上的偶函数满足f(x+4)=f(x),当x∈[0,2]时,f(x)=
,则f[f(2011)]=( )
|
分析:利用函数的周期性,化简f(2011),然后通过偶函数结合分段函数求出所求表达式的值.
解答:解:因为函数满足f(x+4)=f(x),所以函数的周期是4,
所以f(2011)=f(-1),因为函数是偶函数,所以f(2011)=f(-1)=f(1),
因为f(x)=
,
所以f(2011)=f(-1)=f(1)=2,
f[f(2011)]=f(2)=4.
故选D.
所以f(2011)=f(-1),因为函数是偶函数,所以f(2011)=f(-1)=f(1),
因为f(x)=
|
所以f(2011)=f(-1)=f(1)=2,
f[f(2011)]=f(2)=4.
故选D.
点评:本题考查函数的奇偶性,函数的周期,分段函数的值的求法,考查计算能力.

练习册系列答案
相关题目
 定义在R上的奇函数,当
定义在R上的奇函数,当 时,
时, ,给出下列命题:
,给出下列命题: 时,
时,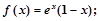 ②函数
②函数 的解集为
的解集为 ④
④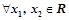 ,都有
,都有
 定义在R上的奇函数,当
定义在R上的奇函数,当 时,
时, ,给出下列命题:
,给出下列命题: 时,
时, ②函数
②函数 的解集为
的解集为 ④
④ ,都有
,都有
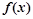 定义在R上的奇函数,当
定义在R上的奇函数,当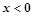 时,
时,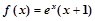 ,给出下列命题:
,给出下列命题: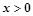 时,
时,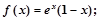 ②函数
②函数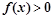 的解集为
的解集为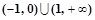 ④
④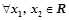 ,都有
,都有