题目内容
已知函数f(x)=ax2-2x-3,
(Ⅰ)当a=1时,方程|f(x)|=m恰有4个解,求m的取值范围.
(Ⅱ)已知
≤a≤1,若f(x)在区间[1,3]上的最大值为M(a),求M(a)的表达式.
(Ⅰ)当a=1时,方程|f(x)|=m恰有4个解,求m的取值范围.
(Ⅱ)已知
| 1 | 3 |
分析:(Ⅰ)当a=1时,函数f(x)=ax2-2x-3,再由方程|f(x)|=m恰有4个解,可得函数y=|f(x)|的图象和直线y=m有4个交点,数形结合可得m的范围.
(Ⅱ)由于函数f(x)=ax2-2x-3的对称轴为x=
,显然1≤
≤3.再分①当1≤
<2 时和②当2≤
≤3 时两种情况,分别求得M(a)的解析式.
(Ⅱ)由于函数f(x)=ax2-2x-3的对称轴为x=
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
解答: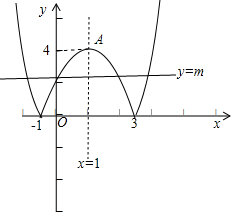 解:(Ⅰ)当a=1时,函数f(x)=ax2-2x-3
解:(Ⅰ)当a=1时,函数f(x)=ax2-2x-3
=x2-2x-3=(x+1)(x-3)=(x-1)2-4,
再由方程|f(x)|=m恰有4个解,
可得函数y=|f(x)|的图象和直线y=m有4个交点.
如图所示:
故m的取值范围为(0,4).
(Ⅱ)由于函数f(x)=ax2-2x-3的对称轴为x=
,
故由
≤a≤1,可得 1≤
≤3.
①当1≤
<2 时,即
<a≤1时,
由二次函数的性质可得f(x)在区间[1,3]上的最大值为M(a)=f(3)=9a-9,
②当2≤
≤3 时,即
≤a≤
时,
由二次函数的性质可得f(x)在区间[1,3]上的最大值为M(a)=f(1)=a-5.
综上可得,M(a)=
.
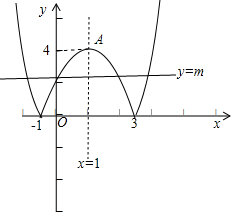 解:(Ⅰ)当a=1时,函数f(x)=ax2-2x-3
解:(Ⅰ)当a=1时,函数f(x)=ax2-2x-3 =x2-2x-3=(x+1)(x-3)=(x-1)2-4,
再由方程|f(x)|=m恰有4个解,
可得函数y=|f(x)|的图象和直线y=m有4个交点.
如图所示:
故m的取值范围为(0,4).
(Ⅱ)由于函数f(x)=ax2-2x-3的对称轴为x=
| 1 |
| a |
故由
| 1 |
| 3 |
| 1 |
| a |
①当1≤
| 1 |
| a |
| 1 |
| 2 |
由二次函数的性质可得f(x)在区间[1,3]上的最大值为M(a)=f(3)=9a-9,
②当2≤
| 1 |
| a |
| 1 |
| 3 |
| 1 |
| 2 |
由二次函数的性质可得f(x)在区间[1,3]上的最大值为M(a)=f(1)=a-5.
综上可得,M(a)=
|
点评:本题主要考查求二次函数在闭区间上的最值,体现了分类讨论、数形结合、等价转化的数学思想,属于中档题.

练习册系列答案
相关题目