题目内容
已知椭圆E: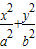 =1(a>b>0)上任意一点到两焦点距离之和为
=1(a>b>0)上任意一点到两焦点距离之和为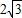 ,离心率为
,离心率为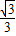 ,左、右焦点分别为F1,F2,点P是右准线上任意一点,过F2作直线PF2的垂线F2Q交椭圆于Q点.
,左、右焦点分别为F1,F2,点P是右准线上任意一点,过F2作直线PF2的垂线F2Q交椭圆于Q点.(1)求椭圆E的标准方程;
(2)证明:直线PQ与直线OQ的斜率之积是定值;
(3)点P的纵坐标为3,过P作动直线l与椭圆交于两个不同点M、N,在线段MN上取点H,满足
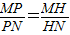 ,试证明点H恒在一定直线上.
,试证明点H恒在一定直线上.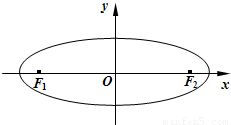
【答案】分析:(1)由题意可得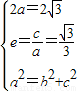 ,解出即可;
,解出即可;
(2)由(1)可知:椭圆的右准线方程为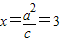 ,设P(3,y),Q(x1,y1),由PF2⊥F2Q,可得
,设P(3,y),Q(x1,y1),由PF2⊥F2Q,可得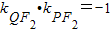 ,利用斜率计算公式可得kPQ•kOQ及
,利用斜率计算公式可得kPQ•kOQ及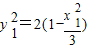 代入化简得直线PQ与直线OQ的斜率之积是定值.
代入化简得直线PQ与直线OQ的斜率之积是定值.
(3)设过P(3,3)的直线l与椭圆交于两个不同点M(x1,y1),N(x2,y2),点H(x,y),由点M,N在椭圆上可得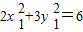 ,
,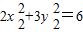 .
.
设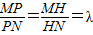 ,则
,则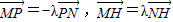 ,可得(3-x1,3-y1)=-λ(x2-3,y2-3),(x-x1,y-y1)=λ(x2-x,y2-y),即可证明6x+9y为定值.
,可得(3-x1,3-y1)=-λ(x2-3,y2-3),(x-x1,y-y1)=λ(x2-x,y2-y),即可证明6x+9y为定值.
解答:解:(1)由题意可得 ,解得
,解得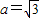 ,c=1,
,c=1,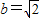
所以椭圆E: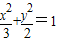 .
.
(2)由(1)可知:椭圆的右准线方程为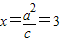 ,
,
设P(3,y),Q(x1,y1),
因为PF2⊥F2Q,所以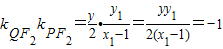 ,
,
所以-y1y=2(x1-1)
又因为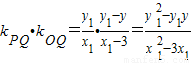 且
且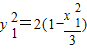 代入化简得
代入化简得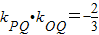 .
.
即直线PQ与直线OQ的斜率之积是定值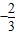 .
.
(3)设过P(3,3)的直线l与椭圆交于两个不同点M(x1,y1),N(x2,y2),点H(x,y),
则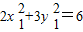 ,
,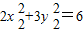 .
.
设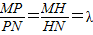 ,则
,则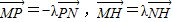 ,
,
∴(3-x1,3-y1)=-λ(x2-3,y2-3),(x-x1,y-y1)=λ(x2-x,y2-y)
整理得 ,
,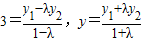 ,
,
∴从而 ,
,
由于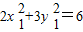 ,
,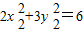 ,∴我们知道
,∴我们知道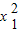 与
与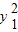 的系数之比为2:3,
的系数之比为2:3, 与
与 的系数之比为2:3.
的系数之比为2:3.
∴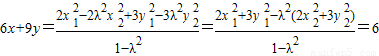 ,
,
所以点H恒在直线2x+3y-2=0上.
点评:本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、向量运算、斜率计算公式等基础知识与基本技能,考查了分析问题和解决问题的能力、推理能力和计算能力.
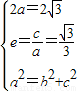 ,解出即可;
,解出即可;(2)由(1)可知:椭圆的右准线方程为
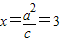 ,设P(3,y),Q(x1,y1),由PF2⊥F2Q,可得
,设P(3,y),Q(x1,y1),由PF2⊥F2Q,可得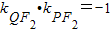 ,利用斜率计算公式可得kPQ•kOQ及
,利用斜率计算公式可得kPQ•kOQ及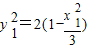 代入化简得直线PQ与直线OQ的斜率之积是定值.
代入化简得直线PQ与直线OQ的斜率之积是定值.(3)设过P(3,3)的直线l与椭圆交于两个不同点M(x1,y1),N(x2,y2),点H(x,y),由点M,N在椭圆上可得
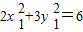 ,
,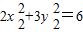 .
.设
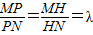 ,则
,则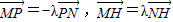 ,可得(3-x1,3-y1)=-λ(x2-3,y2-3),(x-x1,y-y1)=λ(x2-x,y2-y),即可证明6x+9y为定值.
,可得(3-x1,3-y1)=-λ(x2-3,y2-3),(x-x1,y-y1)=λ(x2-x,y2-y),即可证明6x+9y为定值.解答:解:(1)由题意可得
 ,解得
,解得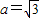 ,c=1,
,c=1,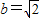
所以椭圆E:
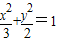 .
.(2)由(1)可知:椭圆的右准线方程为
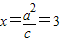 ,
,设P(3,y),Q(x1,y1),
因为PF2⊥F2Q,所以
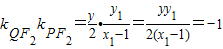 ,
,所以-y1y=2(x1-1)
又因为
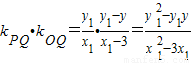 且
且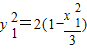 代入化简得
代入化简得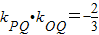 .
.即直线PQ与直线OQ的斜率之积是定值
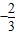 .
.(3)设过P(3,3)的直线l与椭圆交于两个不同点M(x1,y1),N(x2,y2),点H(x,y),
则
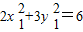 ,
,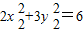 .
.设
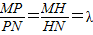 ,则
,则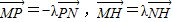 ,
,∴(3-x1,3-y1)=-λ(x2-3,y2-3),(x-x1,y-y1)=λ(x2-x,y2-y)
整理得
 ,
,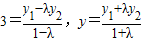 ,
,∴从而
 ,
,由于
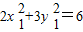 ,
,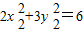 ,∴我们知道
,∴我们知道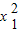 与
与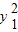 的系数之比为2:3,
的系数之比为2:3, 与
与 的系数之比为2:3.
的系数之比为2:3.∴
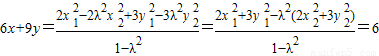 ,
,所以点H恒在直线2x+3y-2=0上.
点评:本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、向量运算、斜率计算公式等基础知识与基本技能,考查了分析问题和解决问题的能力、推理能力和计算能力.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 =1(a>b>o)的离心率e=
=1(a>b>o)的离心率e= ,且经过点(
,且经过点( ,1),O为坐标原点。
,1),O为坐标原点。
 =1(a>b>o)的离心率e=
=1(a>b>o)的离心率e= ,且经过点(
,且经过点( ,1),O为坐标原点。
,1),O为坐标原点。
 =1(a>b>o)的离心率e=
=1(a>b>o)的离心率e= ,且经过点(
,且经过点( ,1),O为坐标原点。
,1),O为坐标原点。
 =1(a>b>0)上任意一点到两焦点距离之和为
=1(a>b>0)上任意一点到两焦点距离之和为 ,离心率为
,离心率为 ,左、右焦点分别为F1,F2,点P是右准线上任意一点,过F2作直线PF2的垂线F2Q交椭圆于Q点.
,左、右焦点分别为F1,F2,点P是右准线上任意一点,过F2作直线PF2的垂线F2Q交椭圆于Q点. 已知椭圆E:
已知椭圆E: =1(a>b>o)的离心率e=
=1(a>b>o)的离心率e= ,且经过点(
,且经过点(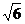 ,1),O为坐标原点。
,1),O为坐标原点。