题目内容
已知椭圆E：
=1（a＞b＞o）的离心率e=
，且经过点（
,1），O为坐标原点。
（Ⅰ）求椭圆E的标准方程；
（Ⅱ）圆O是以椭圆E的长轴为直径的圆，M是直线
x=－4在x轴上方的一点，过M作圆O的两条切线，
切点分别为P、Q，当∠PMQ=60°时，求直线PQ的方程.
【答案】
（1）椭圆的标准方程为：
（2）连接QM，OP，OQ，PQ和MO交于点A，
有题意可得M（-4，m），∵∠PMQ=600
∴∠OMP=300，∵
，
∵m>0,∴m=4,∴M(-4,4)
∴直线OM的斜率
,有MP=MQ,OP=OQ可知OM⊥PQ,
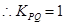,设直线PQ的方程为y=x+n
∵∠OMP=300,∴∠POM=600,∴∠OPA=300,
,即O到直线PQ的距离为
,
(负数舍去),∴PQ的方程为x-y+2=0
【解析】略
练习册系列答案
相关题目
=1（a＞b＞o）的离心率e=
，且经过点（
,1），O为坐标原点。
=1（a＞b＞o）的离心率e=
，且经过点（
,1），O为坐标原点。
=1（a＞b＞0）上任意一点到两焦点距离之和为
，离心率为
，左、右焦点分别为F1，F2，点P是右准线上任意一点，过F2作直线PF2的垂线F2Q交椭圆于Q点．
已知椭圆E：
=1（a＞b＞o）的离心率e=
，且经过点（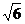
,1），O为坐标原点。