题目内容
（本小题满分14分）
某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响. 已知学生小张只选甲的概率为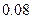
，只选修甲和乙的概率是
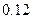，至少选修一门的概率是
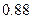，用
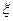表示小张选修的课程门数和没有选修的课程门数的乘积.
（Ⅰ）求学生小张选修甲的概率；
（Ⅱ）记“函数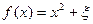
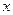为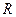
上的偶函数”为事件
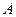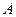，求事件的概率；
（Ⅲ）求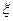的分布列和数学期望。
某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响. 已知学生小张只选甲的概率为
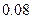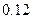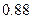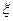，只选修甲和乙的概率是，至少选修一门的概率是，用表示小张选修的课程门数和没有选修的课程门数的乘积.（Ⅰ）求学生小张选修甲的概率；
（Ⅱ）记“函数
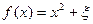
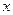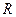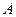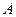为上的偶函数”为事件，求事件的概率；（Ⅲ）求
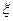的分布列和数学期望。 解：（Ⅰ）设学生小张选修甲、乙、丙的概率分别为、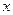
、
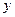依题意得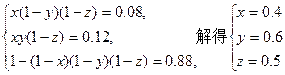
…………3分
所以学生小张选修甲的概率为0.4 …………4分
（Ⅱ）若函数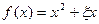
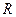为上的偶函数，则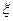="0 " …………5分
当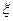=0时，表示小张选修三门功课或三门功课都没选. …………6分
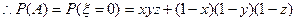
…………7分
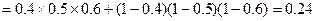
∴事件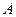的概率为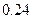
………… 8分
（Ⅲ）依题意知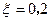
………… 10分
则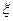的分布列为
…………12分
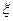∴的数学期望为
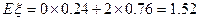…………14分
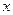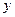、、 依题意得
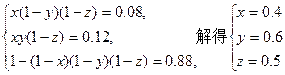…………3分所以学生小张选修甲的概率为0.4 …………4分
（Ⅱ）若函数
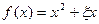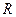为上的偶函数，则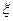="0 " …………5分当
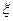=0时，表示小张选修三门功课或三门功课都没选. …………6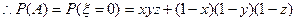分 …………7分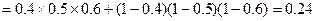 ∴事件
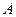的概率为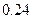 ………… 8分（Ⅲ）依题意知
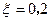………… 10分则
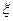的分布列为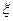 | 0 | 2 |
| P | |  |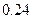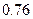
∴
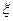的数学期望为 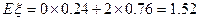…………14分 略
练习册系列答案
相关题目
，
，
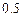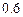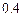。第二次选拔，甲、乙、丙三人合格的概率依次为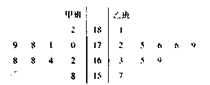
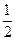，且各局胜负相互独立.求：
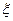的分布列与期望E
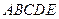五个不同区域，要求同一区域上用同一种颜色的鲜花，相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择．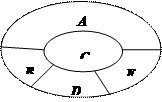
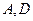区域同时用红色鲜花时，求布置花圃的不同方法的种数；
有两个区域用红色鲜花的概率；
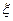为花圃中用红色鲜花布置的区域的个数，求随机变量
.
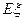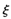的分布列与数学期望.
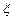服从正态分布
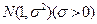．若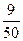
；