题目内容
从1,3,5,7,9五个数字中选2个，0,2,4,6,8五个数字中选3个，能组成多少个无重复数字的五位数？
10 560(个)
解：从5个奇数中选出2个，再从2、4、6、8四个偶数中选出3个，排成五位数，有C52·C43·A55＝4 800(个)．从5个奇数中选出2个，再从2,4,6,8四个偶数中再选出2个，将选出的4个数再选一个做万位数．余下的3个数加上0排在后4个数位上，有C52·C42·C41·A44＝10×6×4×24＝5 760(个)．由分类加法计数原理可知这样的五位数共有C52·C43·C52＋A55·C42·C41·A44＝10 560(个)．
练习册系列答案
相关题目
个专业中，选择
个作为自己的第一、二、三专业志愿，其中甲、乙两个专业不能同时兼报，则该考生有_____________种不同的填报专业志愿的方法（用数字作答）．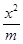
＋
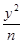＝1表示焦点在x轴上的椭圆的个数为________．