Question

3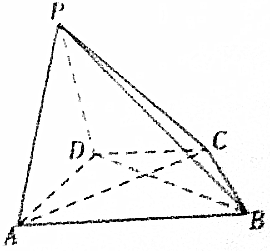．如图所示，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，已知BD=2AD=4，AB=2$\sqrt{5}$，求证：BD⊥平面PAD．

Answer 1

分析 在△ABD中，推出AD⊥BD．通过平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，BD?平面ABCD，证明BD⊥平面PAD．

解答 证明：在△ABD中，由于AD=2，BD=4，AB=2$\sqrt{5}$，
∴AD²+BD²=AB²
∴AD⊥BD．（2分）
又平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，BD?平面ABCD，
∴BD⊥平面PAD．（5分）

点评 本题主要考查了直线与平面垂直的判定，考查了空间想象能力和推理论证能力，属于基本知识的考查．