题目内容
(本小题满分12分)
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
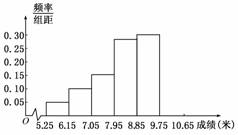 (1) 求这次铅球测试成绩合格的人数;
(1) 求这次铅球测试成绩合格的人数;
(2) 用此次测试结果估计全市毕业生的情况.若从今年的高中毕业生中随机抽取两名,记![]() 表示两人中成绩不合格的人数,求
表示两人中成绩不合格的人数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3) 经过多次测试后,甲成绩在8~10米之间,乙成绩在9.5~10.5米之间,现甲、乙各投掷一次,求甲比乙投掷远的概率.
【试题解析】解:(1)第6小组的频率为1-(0.04+0.10+0.14+0.28+0.30)=0.14,
∴此次测试总人数为![]() (人).
(人).
∴第4、5、6组成绩均合格,人数为(0.28+0.30+0.14)×50=36(人). (4分)
(2)![]() =0,1,2,此次测试中成绩不合格的概率为
=0,1,2,此次测试中成绩不合格的概率为![]() ,∴
,∴![]() ~
~![]() .
.
![]() ,
,![]() ,
,
![]() . (7分)
. (7分)
所求分布列为
| X | 0 | 1 | 2 |
| P |
|
|
|
![]() (9分)
(9分)
(3)设甲、乙各投掷一次的成绩分别为![]() 、
、![]() 米,则基本事件满足的区域为
米,则基本事件满足的区域为

![]() ,事件
,事件![]() “甲比乙投掷远的概率”满足
“甲比乙投掷远的概率”满足
的区域为![]() ,如图所示.
,如图所示.
∴由几何概型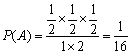 . (12分)
. (12分)

练习册系列答案
相关题目
