题目内容
整数集合内不等式(
)4-x2<(
)2a-2x的解集是{1},求实数a的范围.
| 1 |
| 2 |
| 1 |
| 2 |
分析:由题意,可先考查y=(
)x单调性,将不等式转化为一元二次不等式,再由题设条件整数集合内不等式(
)4-x2<(
)2a-2x的解集是{1},得出参数a所满足的不等式
,解可解出实数a的范围
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
解答:解:由题意(
)4-x2<(
)2a-2x,由于y=(
)x是一个减函数
∴4-x2>2a-2x,即x2-2x+2a-4<0,令f(x)=x2-2x+2a-4
由于整数集合内不等式(
)4-x2<(
)2a-2x的解集是{1},
所以有
,解得2≤a<2.5
答:实数a的范围是2≤a<2.5
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴4-x2>2a-2x,即x2-2x+2a-4<0,令f(x)=x2-2x+2a-4
由于整数集合内不等式(
| 1 |
| 2 |
| 1 |
| 2 |
所以有
|
答:实数a的范围是2≤a<2.5
点评:本题考查指数函数综合题,考查了指数函数的单调性,一元二次函数的性质,解题的关键是将指数不等式转化为一元二次不等式,本题的难点是理解“整数集合内不等式(
)4-x2<(
)2a-2x的解集是{1},”由此知,此不等式的解集中只有整数1,从而推断出x=0,x=2时的函数值都是大于等于0的,这为转化出关于a的不等式组提供了依据.本题考查了理解能力及根据性质转化的能力,考查了转化思想,函数思想
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目
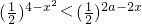 的解集是{1},求实数a的范围.
的解集是{1},求实数a的范围.