题目内容
3. 如图,四棱锥P-ABCD的底面是平行四边形,AB⊥BD,PD⊥平面ABCD,且PD=AB,E为PA的中点.
如图,四棱锥P-ABCD的底面是平行四边形,AB⊥BD,PD⊥平面ABCD,且PD=AB,E为PA的中点.(Ⅰ)求证:CD⊥PB;
(Ⅱ)求证:PC∥平面BED;
(Ⅲ)求二面角E-BD-A的大小.
分析 (Ⅰ)根据线面垂直的性质即可证明CD⊥PB;
(Ⅱ)根据线面平行的判定定理即可证明PC∥平面BED;
(Ⅲ)根据二面角的定义作出二面角,即可求二面角E-BD-A的大小.
解答 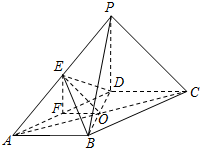 (Ⅰ)证明:∵PD⊥平面ABCD,CD?平面ABCD,
(Ⅰ)证明:∵PD⊥平面ABCD,CD?平面ABCD,
∴CD⊥PD.…(1 分)
∵CD∥AB,AB⊥BD,
∴CD⊥BD.…(2 分)
∵PD∩BD=D,
∴CD⊥平面PBD.…(3 分)
∵PB?平面PBD,
∴CD⊥PB.…(4 分)
(Ⅱ)证明:如图,连接AC,与BD相交于点O,连接EO.
∵四边形ABCD是平行四边形,
∴O为AC的中点.…(5 分)
∵E为PA的中点,
∴EO∥PC.…(6 分)
∵EO?平面BED,PC?平面BED,
∴PC∥平面BED.…(8 分)
(Ⅲ)解:如图,作OF∥AB,交AD于F点,
则F为AD的中点.…(9 分)
∵AB⊥BD,OF∥AB,
∴OF⊥BD.…(10分)
连接EF,则EF∥PD,
∵PD⊥平面ABCD,BD?平面ABCD,
∴PD⊥BD,从而EF⊥BD.
∴BD⊥平面EOF.
∴∠EOF是二面角E-BD-A的平面角.…(11分)
∵PD=AB,$EF=\frac{1}{2}PD$,$OF=\frac{1}{2}AB$,
∴EF=OF.…(12分)
∵EF⊥OF,
∴∠EOF=45°.
∴二面角E-BD-A的大小为45°.…(13分)
点评 本题主要考查空间直线和平面平行,直线和直线垂直的判定,以及二面角的求解,考查学生的运算和推理能力.

练习册系列答案
相关题目
10.已知向量$\overrightarrow{AB}$=(1,2),$\overrightarrow{OB}$=(0,1),则下列各点中在直线AB上的是( )
| A. | (0,3) | B. | (1,1) | C. | (2,4) | D. | (2,5) |
18.已知命题p:?x∈R,x2>0,命题q:?α,β∈R,使tan(α+β)=tanα+tanβ,则下列命题为真命题的是( )
| A. | p∧q | B. | p∨(¬q) | C. | (¬p)∧q | D. | p∧(¬q) |
15.连续掷一正方体骰子(各面的点数分别为1,2,3,4,5,6)两次得到的点数分别为m、n,作向量$\overrightarrow a=(m,n)$,若$\overrightarrow b=(1,-1)$,则$\overrightarrow a$与$\overrightarrow b$的夹角成为直角三角形内角的概率是( )
| A. | $\frac{5}{9}$ | B. | $\frac{7}{12}$ | C. | $\frac{5}{12}$ | D. | $\frac{7}{10}$ |
 如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.
如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC. 在平行四边形ABCD中,E,G分别是BC,DC上的点且$\overrightarrow{BC}$=3$\overrightarrow{BE}$,$\overrightarrow{CD}$=3$\overrightarrow{CG}$,DE与BG交于点O.
在平行四边形ABCD中,E,G分别是BC,DC上的点且$\overrightarrow{BC}$=3$\overrightarrow{BE}$,$\overrightarrow{CD}$=3$\overrightarrow{CG}$,DE与BG交于点O.