题目内容
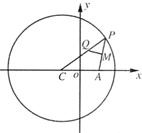 已知C为圆(x+
已知C为圆(x+| 2 |
| 2 |
| MQ |
| AP |
| AP |
| AM |
(1)当点P在圆上运动时,求点Q的轨迹E的方程.
(2)一直线l,原点到l的距离为
| ||
| 2 |
(ii)若直线l与曲线E的两个交点分别为G、H,求△OGH的面积的最大值.
分析:(1)由题设知,MQ⊥AP,QM是P的中垂线,|
|+|
|=|
|+|
|=|
|=r=2
又|
|=2
<2
,
根据椭圆的定义,点Q轨迹是以C(-
,0),A(
,0)为焦点,长轴长为2
的椭圆,由此可知点Q的轨迹方程.
(2)(i)当直线l垂直x轴时,由题意知:l:x=±
,取x=
代入曲线E的方程得:y=±
,即G(
,
),H(
,-
)有两个不同的交点,当直线l不垂直x轴时,设直线l的方程为:y=kx+b,由此入手可知直线l必与椭圆E交于两点
(ii)当直线l垂直x轴时,CH=
=
|GH|×
=
×
×
=
,当直线l不垂直x轴时,设G(x1,y1),H(x2,y2),再由根与系数的关系结合题设条件可求出△OGH的面积的最小值.
| QC |
| QA |
| QC |
| OP |
| CP |
| 3 |
| AC |
| 2 |
| 3 |
根据椭圆的定义,点Q轨迹是以C(-
| 2 |
| 2 |
| 3 |
(2)(i)当直线l垂直x轴时,由题意知:l:x=±
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(ii)当直线l垂直x轴时,CH=
| 3 |
| S | △OGH |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| 4 |
解答:解:(Ⅰ)圆(x+
)2+y2=12的圆心为C(-
,0),半径r=2
∵
•
=0,
=2
,
∴MQ⊥AP,点M是AP的中点,即QM是P的中垂线,连接AQ,则|AQ|=|QP|
∴|
|+|
|=|
|+|
|=|
|=r=2
又|
|=2
<2
,
根据椭圆的定义,点Q轨迹是以C(-
,0),A(
,0)为焦点,长轴长为2
的椭圆,
由c=
,a=
,得b2=1,因此点Q的轨迹方程为
+y2=1.
(Ⅱ)(1)证明:当直线l垂直x轴时,由题意知:l:x=±
,
不妨取x=
代入曲线E的方程得:y=±
即G(
,
),H(
,-
)有两个不同的交点,
当直线l不垂直x轴时,设直线l的方程为:y=kx+b
由题意知:
=
,即b2=
(1+k2)
由
消y得:(2+3k2)x2+6kbx+3b2-3=0
∵△=36k2b2-4(1+3k2)(3b2-3)=12(3k2-b2+1)=27k2+3>0
∴直线l与椭圆E交于两点,综上,直线l必与椭圆E交于两点
(2)由(1)知当直线l垂直x轴时,CH=
=
|GH|×
=
×
×
=
当直线l不垂直x轴时,设G(x1,y1),H(x2,y2),
由(1)知x1+x2=
,x1x2=
|GH|=
=
=
=
=
=
≤
=2(k≠0)
当且仅当9k2=
,即k=±
,则取得“=”,
∴S△OGH=
×
|GH|≤
×
×2=
当k=0时,|GH|=
,S△OGH=
.
综上,△OGH的面积的最小值为
.
| 2 |
| 2 |
| 3 |
∵
| MQ |
| AP |
| AP |
| AM |
∴MQ⊥AP,点M是AP的中点,即QM是P的中垂线,连接AQ,则|AQ|=|QP|
∴|
| QC |
| QA |
| QC |
| OP |
| CP |
| 3 |
又|
| AC |
| 2 |
| 3 |
根据椭圆的定义,点Q轨迹是以C(-
| 2 |
| 2 |
| 3 |
由c=
| 2 |
| 3 |
| x2 |
| 3 |
(Ⅱ)(1)证明:当直线l垂直x轴时,由题意知:l:x=±
| ||
| 2 |
不妨取x=
| ||
| 2 |
| ||
| 2 |
即G(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
当直线l不垂直x轴时,设直线l的方程为:y=kx+b
由题意知:
| |b| | ||
|
| ||
| 2 |
| 3 |
| 4 |
由
|
∵△=36k2b2-4(1+3k2)(3b2-3)=12(3k2-b2+1)=27k2+3>0
∴直线l与椭圆E交于两点,综上,直线l必与椭圆E交于两点
(2)由(1)知当直线l垂直x轴时,CH=
| 3 |
| S | △OGH |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| 4 |
当直线l不垂直x轴时,设G(x1,y1),H(x2,y2),
由(1)知x1+x2=
| -6kb |
| 1+3k2 |
| 3b2-3 |
| 1+3k2 |
| (x1-x2)2+(y1-y2)2 |
=
| (1+k2)[(x1+x2)2-4x1x2] |
=
(1+k2)[
|
=
|
=
3+
|
=
3+
|
3+
|
当且仅当9k2=
| 1 |
| k2 |
| ||
| 3 |
∴S△OGH=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
当k=0时,|GH|=
| 3 |
| 3 |
| 4 |
综上,△OGH的面积的最小值为
| ||
| 2 |
点评:本题考查函数的直线与圆锥问题的综合问题,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
已知直线l:
(t为参数)与圆C:
(θ为参数),则直线l的倾斜角及圆心C的直角坐标分别是( )
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|