题目内容
已知P为圆x2+y2=4上任意一点,Q为点P在x轴上的射影,M为线段PQ的中点,
(1)求点M的轨迹C的方程;
(2)过点E(0,2)的直线l与曲线C交于A、B两点,若点O在以AB为直径的圆上或圆外(O为坐标原点),求直线l的斜率k的取值范围。
(1)求点M的轨迹C的方程;
(2)过点E(0,2)的直线l与曲线C交于A、B两点,若点O在以AB为直径的圆上或圆外(O为坐标原点),求直线l的斜率k的取值范围。
解:(1)设M(x,y),则P(x,2y),
∵点P在圆x2+y2=4上,
∴x2+(2y)2=4,
所以点M的轨迹C的方程为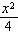 +y2=1;
+y2=1;
(2)依题意,显然l的斜率存在,设l:y=kx+2,
由方程组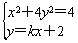 ,消y得(1+4k2)x2+16kx+12=0,
,消y得(1+4k2)x2+16kx+12=0,
∵直线l与C有两交点,
∴△=(16k)2-4×12·(1+4k2)>0,解得k2>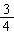 ,
,
且xA+xB=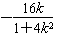 ,xA·xB=
,xA·xB=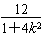 ;
;
又∠AOB为直角或锐角,xA·xB+yA·yB≥0,
即xA·xB+(kxA+2)(kxB+2)≥0,
(1+k2)xA·xB+2k(xA+xB)+4≥0,
所以(1+k2)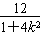 -2k
-2k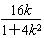 +4≥0,解得k2≤4,
+4≥0,解得k2≤4,
故直线l的斜率k的取值范围是k∈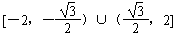 。
。
∵点P在圆x2+y2=4上,
∴x2+(2y)2=4,
所以点M的轨迹C的方程为
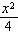 +y2=1;
+y2=1;(2)依题意,显然l的斜率存在,设l:y=kx+2,
由方程组
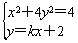 ,消y得(1+4k2)x2+16kx+12=0,
,消y得(1+4k2)x2+16kx+12=0,∵直线l与C有两交点,
∴△=(16k)2-4×12·(1+4k2)>0,解得k2>
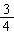 ,
,且xA+xB=
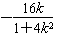 ,xA·xB=
,xA·xB=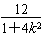 ;
;又∠AOB为直角或锐角,xA·xB+yA·yB≥0,
即xA·xB+(kxA+2)(kxB+2)≥0,
(1+k2)xA·xB+2k(xA+xB)+4≥0,
所以(1+k2)
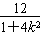 -2k
-2k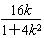 +4≥0,解得k2≤4,
+4≥0,解得k2≤4,故直线l的斜率k的取值范围是k∈
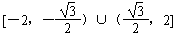 。
。
练习册系列答案
相关题目