题目内容
在直角坐标系xOy中,以坐标原点O为圆心的圆与直线: 相切.
相切.(1)求圆O的方程;
(2)若圆O上有两点M、N关于直线x+2y=0对称,且
 ,求直线MN的方程;
,求直线MN的方程;(3)圆O与x轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,求
 的取值范围.
的取值范围.
【答案】分析:(1)利用点到直线的距离公式求出半径r,从而求得圆O的方程.
(2)用点斜式设出MN的方程为y=2x+b,由条件求出圆心O到直线MN的距离等于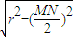 =1,由1=
=1,由1=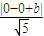 ,
,
求出b的值,即可得到MN的方程.
(3)由题意可得|PA|•|PB|=|PO|2 ,设点P(x,y),代入化简可得x2=y2+2.由点P在圆内可得 x2+y2<4,可得0≤y2<1.化简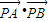 =2(y2-1),从而求得
=2(y2-1),从而求得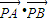 的取值范围.
的取值范围.
解答:解:(1)半径r=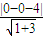 =2,故圆O的方程为 x2+y2=4.
=2,故圆O的方程为 x2+y2=4.
(2)∵圆O上有两点M、N关于直线x+2y=0对称,故MN的斜率等于直线x+2y=0斜率的负倒数,等于2,
设MN的方程为y=2x+b,即2x-y+b=0.
由弦长公式可得,圆心O到直线MN的距离等于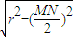 =1.
=1.
由点到直线的距离公式可得 1=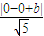 ,b=±
,b=±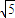 ,故MN的方程为2x-y±
,故MN的方程为2x-y±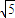 =0.
=0.
(3)圆O与x轴相交于A(-2,0)、B(2,0)两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,
∴|PA|•|PB|=|PO|2 ,设点P(x,y),
则有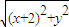 •
•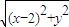 =x2+y2,化简可得 x2=y2+2.
=x2+y2,化简可得 x2=y2+2.
由点P在圆内可得 x2+y2<4,故有 0≤y2<1.
∵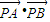 =(-2-x,-y)•(2-x,-y)=x2+y2-4=2(y2-1)∈[-2,0).
=(-2-x,-y)•(2-x,-y)=x2+y2-4=2(y2-1)∈[-2,0).
即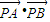 的取值范围是[-2,0).
的取值范围是[-2,0).
点评:本题主要考查等比数列的定义和性质,直线和圆的位置关系,两个向量的数量积的定义,属于中档题.
(2)用点斜式设出MN的方程为y=2x+b,由条件求出圆心O到直线MN的距离等于
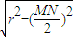 =1,由1=
=1,由1=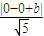 ,
,求出b的值,即可得到MN的方程.
(3)由题意可得|PA|•|PB|=|PO|2 ,设点P(x,y),代入化简可得x2=y2+2.由点P在圆内可得 x2+y2<4,可得0≤y2<1.化简
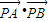 =2(y2-1),从而求得
=2(y2-1),从而求得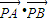 的取值范围.
的取值范围.解答:解:(1)半径r=
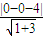 =2,故圆O的方程为 x2+y2=4.
=2,故圆O的方程为 x2+y2=4.(2)∵圆O上有两点M、N关于直线x+2y=0对称,故MN的斜率等于直线x+2y=0斜率的负倒数,等于2,
设MN的方程为y=2x+b,即2x-y+b=0.
由弦长公式可得,圆心O到直线MN的距离等于
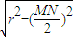 =1.
=1.由点到直线的距离公式可得 1=
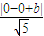 ,b=±
,b=±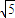 ,故MN的方程为2x-y±
,故MN的方程为2x-y±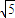 =0.
=0.(3)圆O与x轴相交于A(-2,0)、B(2,0)两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,
∴|PA|•|PB|=|PO|2 ,设点P(x,y),
则有
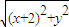 •
•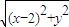 =x2+y2,化简可得 x2=y2+2.
=x2+y2,化简可得 x2=y2+2.由点P在圆内可得 x2+y2<4,故有 0≤y2<1.
∵
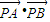 =(-2-x,-y)•(2-x,-y)=x2+y2-4=2(y2-1)∈[-2,0).
=(-2-x,-y)•(2-x,-y)=x2+y2-4=2(y2-1)∈[-2,0).即
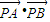 的取值范围是[-2,0).
的取值范围是[-2,0).点评:本题主要考查等比数列的定义和性质,直线和圆的位置关系,两个向量的数量积的定义,属于中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
 如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为
如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为