题目内容
等差数列{an}的公差d不为0,Sn是其前n项和,给出下列命题:
①若d<0,且S3=S8,则S5和S6都是{Sn}中的最大项;
②给定n,对于一切 ,都有
,都有 ;
;
③若d>0,则{Sn}中一定有最小的项;
④存在 ,使
,使 和
和 同号。
同号。
其中正确命题的个数为
A.4 B.3 C.2 D.1
【答案】
B
【解析】
试题分析:因为{ an }成等差数列,所以其前n项和是关于n的二次函数的形式且缺少常数项。
d<0说明二次函数开口向下,又S3=S8,说明函数关于直线x=5.5对称,所以S5和S6都是最大项,①正确;
同理,若d>0,说明函数是递增的,故{Sn}中一定存在最小的项,③正确;
而②是等差中项的推广,正确;
对于④,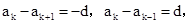 因为d≠0,所以二者异号.
因为d≠0,所以二者异号.
所以正确命题的个数为3个.
故选B。
考点:本题主要考查等差数列的通项公式、求和公式,等差数列的性质。
点评:中档题,等差数列与一次函数密切相关,特别是其前n项和公式是关于n的二次函数的形式且缺少常数项(d不为0),所以可结合二次函数性质解题。

练习册系列答案
相关题目