题目内容
如果一个数列的各项均为实数,且从第二项起开始,每一项的平方与它前一项的平方的差都是同一个常数,则称该数列为等方差数列,这个常数叫做这个数列的公方差.
(1)若数列{bn}是等方差数列,b1=1,b2=3,求b7;
(2)是否存在一个非常数数列的等差数列或等比数列,同时也是等方差数列?若存在,求出这个数列;若不存在,说明理由.
(3)若正项数列{an}是首项为2、公方差为4的等方差数列,数列{
}的前n项和为Tn,是否存在正整数p,q,使不等式Tn>
-1对一切n∈N*都成立?若存在,求出p,q的值;若不存在,说明理由.
(1)若数列{bn}是等方差数列,b1=1,b2=3,求b7;
(2)是否存在一个非常数数列的等差数列或等比数列,同时也是等方差数列?若存在,求出这个数列;若不存在,说明理由.
(3)若正项数列{an}是首项为2、公方差为4的等方差数列,数列{
| 1 |
| an |
| pn+q |
分析:(1)利用等方差数列的定义求出公方差,即可求得b7的值;
(2)若数列{an}是等差数列,设an=an+b(a,b∈R),利用{an}也是等方差数列,应有an2-an-12=k(k为与n无关的常数),从而可得an=b必为一常数数列;若数列{an}是等比数列,利用{an}也是等方差数列,应有an2-an-12=k(k为与n无关的常数),可得q=±1,再验证即可;
(3)先求数列{
}的前n项和,再假设存在正整数p,q,使不等式Tn>
-1对一切n∈N*都成立,猜想p=q=1,再进行证明.
(2)若数列{an}是等差数列,设an=an+b(a,b∈R),利用{an}也是等方差数列,应有an2-an-12=k(k为与n无关的常数),从而可得an=b必为一常数数列;若数列{an}是等比数列,利用{an}也是等方差数列,应有an2-an-12=k(k为与n无关的常数),可得q=±1,再验证即可;
(3)先求数列{
| 1 |
| an |
| pn+q |
解答:解:(1)由{bn}是等方差数列,b1=1,b2=3,有公方差d=32-12=8,------(1分)
于是b72=1+(7-1)×8=49,∴b7=±7------------------------------(3分)
(2)若数列{an}是等差数列,设an=an+b(a,b∈R),则an2=a2n2+2abn+b2,
要使{an}也是等方差数列,应有an2-an-12=k(k为与n无关的常数),得a2=0,即a=0,这时an=b必为一常数数列,因此不存在一个非常数数列的等差数列,同时也是等方差数列.-----(5分)
若数列{an}是等比数列,设an=a1qn-1(q为公比且q≠0),则an2=a12q2n-2,
要使{an}也是等方差数列,应有an2-an-12=k(k为与n无关的常数),即a12q2n-2-a12q2n-4=a12q2n-4(q2-1)=k,所以必有q2=1,q=±1,----------(7分)
当q=1时,数列{an}是常数数列,故舍去
当q=-1时,所以存在一个非常数数列的等比数列,同时也是等方差数列,其公比q=-1.--(9分)
(3)由于{an}是首项为2,公方差为4的等方差数列,∴an2=a12+(n-1)d=4+4(n-1)=4n,
∴an=2
,------(10分)
∴数列{
}的前n项和为:Tn=
(
+
+
+…+
)---(11分)
假设存在正整数p,q使不等式
(
+
+
+…+
)>
-1对一切n∈N*都成立.
即
+
+
+…+
>2(
-1)
当n=1时,1>2(
-1),∴p+q<
,又p,q为正整数,∴p=q=1.--(13分)
下证明:
+
+
+…+
>2(
-1)对一切n∈N*都成立.
由于
=
>
=2(
-
)(n∈N*)
所以
+
+
+…+
>2[(
-1)+(
-
)+…+(
-
)]=2(
-1).(16分)
于是b72=1+(7-1)×8=49,∴b7=±7------------------------------(3分)
(2)若数列{an}是等差数列,设an=an+b(a,b∈R),则an2=a2n2+2abn+b2,
要使{an}也是等方差数列,应有an2-an-12=k(k为与n无关的常数),得a2=0,即a=0,这时an=b必为一常数数列,因此不存在一个非常数数列的等差数列,同时也是等方差数列.-----(5分)
若数列{an}是等比数列,设an=a1qn-1(q为公比且q≠0),则an2=a12q2n-2,
要使{an}也是等方差数列,应有an2-an-12=k(k为与n无关的常数),即a12q2n-2-a12q2n-4=a12q2n-4(q2-1)=k,所以必有q2=1,q=±1,----------(7分)
当q=1时,数列{an}是常数数列,故舍去
当q=-1时,所以存在一个非常数数列的等比数列,同时也是等方差数列,其公比q=-1.--(9分)
(3)由于{an}是首项为2,公方差为4的等方差数列,∴an2=a12+(n-1)d=4+4(n-1)=4n,
∴an=2
| n |
∴数列{
| 1 |
| an |
| 1 |
| 2 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
假设存在正整数p,q使不等式
| 1 |
| 2 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| pn+q |
即
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| pn+q |
当n=1时,1>2(
| p+q |
| 9 |
| 4 |
下证明:
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| n+1 |
由于
| 1 | ||
|
| 2 | ||||
|
| 2 | ||||
|
| n+1 |
| n |
所以
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 2 |
| 3 |
| 2 |
| n+1 |
| n |
| n+1 |
点评:本题考查新定义,考查等差数列与等比数列的综合,考查学生分析解决问题的能力,正确理解新定义是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
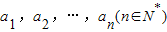 ,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”
,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换” 的前n项和为Tn,是否存在正整数p,q,使不等式
的前n项和为Tn,是否存在正整数p,q,使不等式 对一切n∈N*都成立?若存在,求出p,q的值;若不存在,说明理由.
对一切n∈N*都成立?若存在,求出p,q的值;若不存在,说明理由.