题目内容
若各项都是实数的数列从第二项起,每一项与它前一项的平方差是同一常数,则称该数列为等方差数列,这个常数叫这个数列的公方差.
(Ⅰ)若数列{an}是等差数列,前n项和为Tn,并且an2=T2n-1,求通项an;
(Ⅱ)若数列{an}是首项为2,公方差为2的等方差数列,数列{bn}的前n项和为Sn,且an2=2n+1bn.2n•Sn>m•2n-2an2对?n∈N*恒成立,求m的取值范围.
(Ⅰ)若数列{an}是等差数列,前n项和为Tn,并且an2=T2n-1,求通项an;
(Ⅱ)若数列{an}是首项为2,公方差为2的等方差数列,数列{bn}的前n项和为Sn,且an2=2n+1bn.2n•Sn>m•2n-2an2对?n∈N*恒成立,求m的取值范围.
分析:(Ⅰ)利用an2=T2n-1,根据新定义,可求通项an;
(Ⅱ)由{an}是首项为2,公方差为2的等方差数列,即{an2}为首项为4,公差为2的等差数列,从而可求数列{bn}的前n项和为Sn,从而不等式2n•Sn>m•2n-2an2即3•2n-(n+3)>m•2n-4n-4,分离参数可得m-3<
恒成立,利用归纳法,可求m的取值范围.
(Ⅱ)由{an}是首项为2,公方差为2的等方差数列,即{an2}为首项为4,公差为2的等差数列,从而可求数列{bn}的前n项和为Sn,从而不等式2n•Sn>m•2n-2an2即3•2n-(n+3)>m•2n-4n-4,分离参数可得m-3<
| 3n+1 |
| 2n |
解答:解:(Ⅰ)an2=T2n-1=
=
=(2n-1)•an
∴an[an-(2n-1)]=0
∴an=2n-1,或an=0…(4分)
(Ⅱ)由{an}是首项为2,公方差为2的等方差数列,即{an2}为首项为4,公差为2的等差数列,
∴an2=4+2(n-1)=2n+2…(6分)
由an2=2n+1bn得bn=
=
=
∴Sn=1+
+
+…+
①;
Sn=
+
+…+
+
②
①-②可得
Sn=1+
+
+…+
-
=
+1-
-
=
-
-
∴Sn=3-
…(9分)
不等式2n•Sn>m•2n-2an2即3•2n-(n+3)>m•2n-4n-4
也即(m-3)•2n<3n+1,即需要m-3<
恒成立
由于n=1,2,3时,3n+1>2n;n=4时,3n+1<2n;
假设n=k(k≥4)时,3k+1<2k,
那么2k+1=2•2k>2(3k+1)=3(k+1)+1+(3k-2)>3(k+1)+1,
归纳知:n≥4时,3k+1<2k,
>0,∴m-3≤0,
故m的取值范围为m≤3…(13分)
| (2n-1)(a1+a2n-1) |
| 2 |
| (2n-1)•2an |
| 2 |
∴an[an-(2n-1)]=0
∴an=2n-1,或an=0…(4分)
(Ⅱ)由{an}是首项为2,公方差为2的等方差数列,即{an2}为首项为4,公差为2的等差数列,
∴an2=4+2(n-1)=2n+2…(6分)
由an2=2n+1bn得bn=
| an2 |
| 2n+1 |
| 2n+2 |
| 2n+1 |
| n+1 |
| 2n |
∴Sn=1+
| 3 |
| 22 |
| 4 |
| 23 |
| n+1 |
| 2n |
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
| n+1 |
| 2n+1 |
①-②可得
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| n+1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n |
| n+1 |
| 2n+1 |
| 3 |
| 2 |
| 1 |
| 2n |
| n+1 |
| 2n+1 |
∴Sn=3-
| n+3 |
| 2n |
不等式2n•Sn>m•2n-2an2即3•2n-(n+3)>m•2n-4n-4
也即(m-3)•2n<3n+1,即需要m-3<
| 3n+1 |
| 2n |
由于n=1,2,3时,3n+1>2n;n=4时,3n+1<2n;
假设n=k(k≥4)时,3k+1<2k,
那么2k+1=2•2k>2(3k+1)=3(k+1)+1+(3k-2)>3(k+1)+1,
归纳知:n≥4时,3k+1<2k,
| 3n+1 |
| 2n |
故m的取值范围为m≤3…(13分)
点评:本题考查新定义,等差数列的性质、通项、前n项和公式,错位相减法求和,恒成立,数学归纳法,探索分析和推理解决问题的能力.

练习册系列答案
相关题目
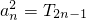 ,求通项an;
,求通项an;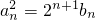 .
.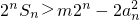 对?n∈N*恒成立,求m的取值范围.
对?n∈N*恒成立,求m的取值范围.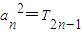 ,求通项an;
,求通项an;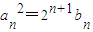 .
.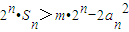 对?n∈N*恒成立,求m的取值范围.
对?n∈N*恒成立,求m的取值范围.