题目内容
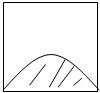如图所示，墙上挂有一块边长为2的正方形木板，上面画有振幅为1的正弦曲线半个周期的图案（阴影部分）．某人向此板投镖，假设每次都能击中木板并且击中木板上每个点的可能性都一样，则他击中阴影部分的概率是分析：先建立直角坐标系，用定积分求得阴影部分的面积，再求得正方形的面积，最后代入几何概型的概率公式求解．
解答：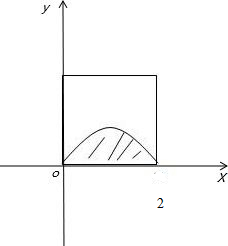
解：建立如图所示坐标系，
则阴影部分的面积为：|∫02sinxdx|=|cosx|02|=1-cos2
正方形面积为4
根据几何概型的概率公式得：P=
=
故答案为：
解：建立如图所示坐标系，则阴影部分的面积为：|∫02sinxdx|=|cosx|02|=1-cos2
正方形面积为4
根据几何概型的概率公式得：P=
| 阴影部分的面积 |
| 正方形的面积 |
| 1-cos2 |
| 4 |
故答案为：
| 1-cos2 |
| 4 |
点评：本题主要考查几何概型的概率的求法，基本思路是，先定类型，是长度，面积还是体积类型，然后，分别求得所研究的区域，再用公式求解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
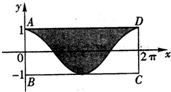如图所示，墙上挂有一长为2π，宽为2的矩形木板ABCD，它的阴影部分是由函数y=cosx，x∈[0，2π]的图象和直线y=1围成的图形．某人向此板投镖，假设每次都能投中木板，且击中木板上每个点的可能性都一样，则他击中阴影部分的概率是
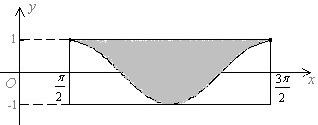如图所示，墙上挂有一长为2π宽为2的矩形木板ABCD，它的阴影部分是由y=sinx，
的图象和直线y=1围成的图形，某人向此板投飞镖，假设每次都能击中木板，且击中木板上每一点的可能性相同，则他击中阴影部分的概率是 ．
的图象和直线y=1围成的图形，某人向此板投飞镖，假设每次都能击中木板，且击中木板上每一点的可能性相同，则他击中阴影部分的概率是 ．