题目内容
【题目】作出下列函数的大致图像,并写出函数的单调区间和值域.
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .
.
【答案】(1)增区间:![]() ,值域:R;
,值域:R;
(2)增区间:![]() 和
和![]() ,减区间:
,减区间:![]() ,值域:
,值域:![]() ;
;
(3)减区间:![]() 和
和![]() ,增区间:
,增区间:![]() 和
和![]() ,值域:
,值域:![]() ;
;
(4)减区间:![]() 和
和![]() ,增区间:
,增区间:![]() 和
和![]() ,值域:
,值域:![]() ,大致图像见解析
,大致图像见解析
【解析】
(1)由![]() ,由对称性即可作出图像,结合图像即可求出单调性、值域.
,由对称性即可作出图像,结合图像即可求出单调性、值域.
(2)将函数化为![]() ,利用幂函数的图像,由平移即可作出图像,结合图像即可求出单调性、值域.
,利用幂函数的图像,由平移即可作出图像,结合图像即可求出单调性、值域.
(3)由![]() ,通过图像的翻折变化即可作出图像,结合图像即可求出单调性、值域.
,通过图像的翻折变化即可作出图像,结合图像即可求出单调性、值域.
(4)由![]() ,去绝对值,描点即可作出大致图像,结合图像即可求出单调性、值域.
,去绝对值,描点即可作出大致图像,结合图像即可求出单调性、值域.
(1)函数![]() 的图象如图所示:
的图象如图所示:
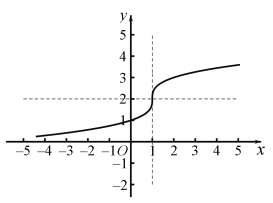
函数在![]() 上为增函数,值域:
上为增函数,值域:![]() .
.
(2)![]() ,图象如图所示:
,图象如图所示:
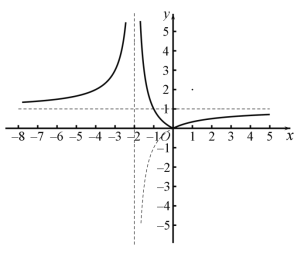
函数在![]() 和
和![]() 为增函数,在
为增函数,在![]() 为减函数,
为减函数,
值域为:![]() .
.
(3)![]() ,图象如图所示:
,图象如图所示:
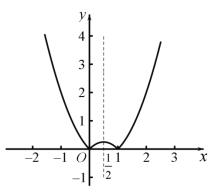
函数在![]() 和
和![]() 为减函数,在
为减函数,在![]() 和
和![]() 为增函数.
为增函数.
值域为:![]() ;
;
(4)![]()
,
函数在![]() 和
和![]() 为减函数,在
为减函数,在![]() 和
和![]() 为增函数,
为增函数,
值域为:![]() .
.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
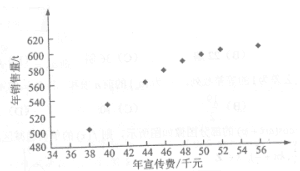
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案【题目】(本小题满分12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() =
=![]() ,
,![]() =
=![]()
![]()
(Ⅰ)根据散点图判断,![]() 与
与![]() ,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);
,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(III)已知这种产品的年利z与x,y的关系为![]() ,根据(Ⅱ)的结果回答下列问题:
,根据(Ⅱ)的结果回答下列问题:
(Ⅰ)当年宣传费![]() 时,年销售量及年利润的预报值时多少?
时,年销售量及年利润的预报值时多少?
(Ⅱ)当年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
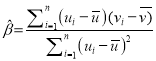 ,
,![]()
【题目】某省级示范高中高三年级对考试的评价指标中,有“难度系数”“区分度”和“综合”三个指标,其中,难度系数![]() ,区分度
,区分度![]() ,综合指标
,综合指标![]() .以下是高三年级 6 次考试的统计数据:
.以下是高三年级 6 次考试的统计数据:
i | 1 | 2 | 3 | 4 | 5 | 6 |
难度系数 xi | 0.66 | 0.72 | 0.73 | 0.77 | 0.78 | 0.84 |
区分度 yi | 0.19 | 0.24 | 0.23 | 0.23 | 0.21 | 0.16 |
(I) 计算相关系数![]() ,若
,若![]() ,则认为
,则认为![]() 与
与![]() 的相关性强;通过计算相关系数
的相关性强;通过计算相关系数![]() ,能否认为
,能否认为![]() 与
与![]() 的相关性很强(结果保留两位小数)?
的相关性很强(结果保留两位小数)?
(II) 根据经验,当![]() 时,区分度
时,区分度![]() 与难度系数
与难度系数![]() 的相关性较强,从以上数据中剔除(0.7,0.8)以外的
的相关性较强,从以上数据中剔除(0.7,0.8)以外的![]() 值,即
值,即![]() .
.
(i) 写出剩下 4 组数据的线性回归方程(![]() 保留两位小数);
保留两位小数);
(ii) 假设当![]() 时,
时,![]() 与
与![]() 的关系依从(i)中的回归方程,当
的关系依从(i)中的回归方程,当![]() 为何值时,综合指标
为何值时,综合指标![]() 的值最大?
的值最大?
参考数据:
![]()
参考公式:
相关系数
回归方程中斜率和截距的最小二乘估计公式为