题目内容
6.函数f(x)=$\frac{{2{{cos}^2}(x-1)-x}}{x-1}$,其图象的对称中心是( )| A. | (-1,1) | B. | (1,-1) | C. | (1,1) | D. | (0,-1) |
分析 f(x)=$\frac{{2{{cos}^2}(x-1)-x}}{x-1}$得到y+1=$\frac{cos2(x-1)}{x-1}$设y′=y+1,x′=x-1得到y′=$\frac{cos2x′}{x′}$为奇函数,即可得出结论.
解答 解:f(x)=$\frac{{2{{cos}^2}(x-1)-x}}{x-1}$得到y+1=$\frac{cos2(x-1)}{x-1}$
设y′=y+1,x′=x-1得到y′=$\frac{cos2x′}{x′}$为奇函数,
则对称中心为(0,0)即y′=0,x′=0得到y=-1,x=1,
所以函数y的对称中心为(1,-1).
故选:B.
点评 本题考查图象的对称中心,将函数正确变形是关键.

练习册系列答案
相关题目
14.已知函数f(x)=ex-mx-exlnx+1,且定义域为(0,e],若函数f(x)在定义域内有两个极值点,则m的取值范围为( )
| A. | [0,ee-2e] | B. | (0,ee-2e] | C. | (0,ee-2e) | D. | (ee-2e,+∞) |
1.设函数f(x)=2x,则如图所示的函数图象( )
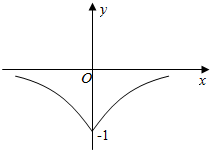

| A. | y=f(|x|) | B. | y=-|f(x)| | C. | y=-f(-|x|) | D. | y=f(-|x|) |
11.已知|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=5,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,则|$\overrightarrow{a}$-$\overrightarrow{b}$|等于( )
| A. | 5$\sqrt{3}$ | B. | $\frac{5\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 5 |
18.已知数据x1,x2,x3,…,xn是武汉市n(n≥3,n∈N*)个普通职工的2014年的年收入,设这n个数据的中位数为x,平均数为y,方差为z,如果再加上比尔.盖茨的2014年的年收入xn+1(约80亿美元),则这n+1个数据中,下列说法正确的是( )
| A. | 年收入平均数大大增大,中位数一定变大,方差可能不变 | |
| B. | 年收入平均数大大增大,中位数可能不变,方差变大 | |
| C. | 年收入平均数大大增大,中位数可能不变,方差也不变 | |
| D. | 年收入平均数可能不变,中位数可能不变,方差可能不变 |
15.设函数f(x)=${(\frac{1}{2})}^{lnx}$-|lnx-2|的所有零点之积为m,则m所在的区间为( )
| A. | (1,e) | B. | (e,e2) | C. | (e2,e3) | D. | (e3,e4) |