题目内容
（2012•绵阳一模）若函数f（x）=-x3+bx在区间（O，1）上单调递增，且方程f（x）=0的根都在区间[-2，2]上，则实数b的取值范围为（ ）
分析：把函数在区间（0，1）的单调递增转化成导函数在（0，1）恒大于0，然后求出方程f（x）=0的根，使根都在区间[-2，2]内即可得答案．
解答：解：∵函数f（x）在区间（0，1）上单调递增，
∴其导数f'（x）=-3x2+b＞0在（0，1）上恒成立
即b＞3x2在（0，1）上恒成立，可得b≥3
而f（x）=-x3+bx=-x（x2-b）=0的三个根为0，±
要使方程f（x）=0的根都在区间[-2，2]内
只需
≤2，解得b≤4
综上可得：3≤b≤4
故选D
∴其导数f'（x）=-3x2+b＞0在（0，1）上恒成立
即b＞3x2在（0，1）上恒成立，可得b≥3
而f（x）=-x3+bx=-x（x2-b）=0的三个根为0，±
| b |
要使方程f（x）=0的根都在区间[-2，2]内
只需
| b |
综上可得：3≤b≤4
故选D
点评：本题考查函数与方程的综合运用，以及利用导数研究函数的单调性，属基础题．
练习册系列答案
相关题目
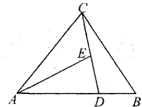（2012•绵阳一模）如图，在△ABC中，AD=2DB，DE=EC，若