题目内容
(2012•绵阳一模)已知{an}是递增数列,且对任意的n∈N*都有an=n2+2
sinθ•n(θ∈[0,2π])恒成立,则角θ的取值范围是
| 3 |
[0,
]∪[
,2π]
| 4π |
| 3 |
| 5π |
| 3 |
[0,
]∪[
,2π]
.| 4π |
| 3 |
| 5π |
| 3 |
分析:根据已知条件{an}是递增数列,且对任意的n∈N*都有an=n2+2
sinθ•n(θ∈[0,2π])恒成立,可以推出an+1≥an,推出一个关于n,θ的不等式,转化为不等式的恒成立问题,从而进行求解;
| 3 |
解答:解:∵{an}是递增数列,且对任意的n∈N*都有an=n2+2
sinθ•n(θ∈[0,2π])恒成立,
∴an+1≥an,对任意的n∈N*都成立,
∴(n+1)2+2
sinθ•(n+1)-n2-2
sinθ•n,
∴2n+1+2
sinθ≥0,转化为2
sinθ≥-2n-1,恒成立,因为n≥1,n∈N*,
∴-2n-1≥-3,
∴2
sinθ≥-3,解得sinθ≥-
,∵θ∈[0,2π]
解得0≤θ≤
,或
≤θ≤2π,
故答案为:[0,
]∪[
,2π];
| 3 |
∴an+1≥an,对任意的n∈N*都成立,
∴(n+1)2+2
| 3 |
| 3 |
∴2n+1+2
| 3 |
| 3 |
∴-2n-1≥-3,
∴2
| 3 |
| ||
| 2 |
解得0≤θ≤
| 4π |
| 3 |
| 5π |
| 3 |
故答案为:[0,
| 4π |
| 3 |
| 5π |
| 3 |
点评:本题考查的知识点是数列的函数特性,二次函数的性质,其中根据已知条件将问题转化为一个不等式恒成立问题是解答本题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
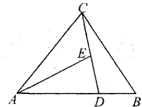 (2012•绵阳一模)如图,在△ABC中,AD=2DB,DE=EC,若
(2012•绵阳一模)如图,在△ABC中,AD=2DB,DE=EC,若