题目内容
设a、b是两条不重合的直线,α、β是两个不重合的平面,则下列命题中不正确的一个是( )
分析:由垂直于同一直线的两个平面平行,可判断A的真假;
由线面垂直的性质定理,可判断B的真假;
由线面垂直的定义(性质),可判断C的真假;
由线面平行的几何特征,我们可以分析出a∥b或a,b异面,进而判断出D的真假;
由线面垂直的性质定理,可判断B的真假;
由线面垂直的定义(性质),可判断C的真假;
由线面平行的几何特征,我们可以分析出a∥b或a,b异面,进而判断出D的真假;
解答:解:若a⊥α,a⊥β,由垂直于同一直线的两个平面平行,可得α∥β,故A正确;
若a⊥β,b⊥β,由线面垂直的性质定理,可得a∥b,故B正确;
若b⊥β,a⊆β,由线面垂直的定义(性质),可得a⊥b,故C正确;
若a∥β,b⊆β,则a与b没有交点,故a∥b或a,b异面,故D不正确.
故选D
若a⊥β,b⊥β,由线面垂直的性质定理,可得a∥b,故B正确;
若b⊥β,a⊆β,由线面垂直的定义(性质),可得a⊥b,故C正确;
若a∥β,b⊆β,则a与b没有交点,故a∥b或a,b异面,故D不正确.
故选D
点评:本题以命题的真假判断为载体考查了空间直线与直线之间的位置关系,直线与平面之间的位置关系和平面与平面之间的位置关系,熟练掌握空间线面关系的定义、判定及几何特征是解答的关键.

练习册系列答案
相关题目
 是两个不重合的平面,则下列命题中不正确的一个是
是两个不重合的平面,则下列命题中不正确的一个是 则
则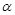 ∥
∥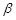 B.若
B.若 ,则
,则 ∥
∥
 则
则 D.若
D.若 ,则
,则