题目内容
已知函数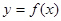 的定义域为
的定义域为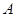 ,若常数
,若常数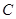 满足:对任意正实数
满足:对任意正实数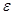 ,总存在
,总存在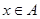 ,使得
,使得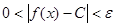 成立,则称
成立,则称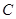 为函数
为函数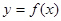 的“渐近值”.现有下列三个函数:①
的“渐近值”.现有下列三个函数:① 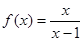 ;②
;② 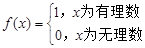 ;③
;③ 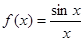 .其中以数“1”为渐近值的函数个数为( )
.其中以数“1”为渐近值的函数个数为( )
| A.0 | B.1 | C.2 | D.3 |
C
解析试题分析:依题意函数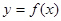 的“渐近值” 对任意正实数
的“渐近值” 对任意正实数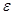 ,总存在
,总存在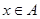
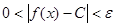 ,即可理解为函数的值域趋近一个常数.由
,即可理解为函数的值域趋近一个常数.由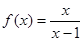
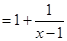 .所以
.所以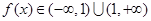 .故①存在C=1符合条件.由
.故①存在C=1符合条件.由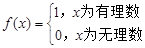 ,
,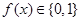 .假设存在C,对任意正实数
.假设存在C,对任意正实数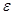 ,总存在
,总存在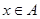 使得
使得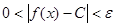 即
即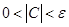 或
或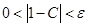 .对于一个常数C没办法满足任意的正数
.对于一个常数C没办法满足任意的正数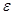 .所以②不符合.
.所以②不符合.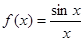 的图象如图所示.所以存在C=0,符合条件.所以①③正确.故选C.
的图象如图所示.所以存在C=0,符合条件.所以①③正确.故选C.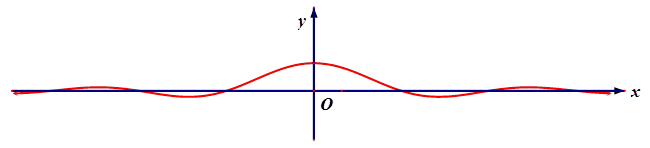
考点:1.新定义.2.函数的范围.3.函数图象.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
定义在R上的函数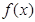 和
和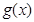 的导函数分别为
的导函数分别为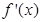 ,
,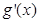 ,则下面结论正确的是( )
,则下面结论正确的是( )
①若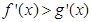 ,则函数
,则函数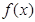 的图象在函数
的图象在函数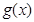 的图象上方;
的图象上方;
②若函数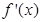 与
与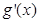 的图象关于直线
的图象关于直线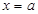 对称,则函数
对称,则函数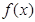 与
与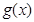 的图象关于点(
的图象关于点(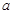 ,0)对称;
,0)对称;
③函数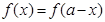 ,则
,则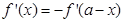 ;
;
④若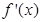 是增函数,则
是增函数,则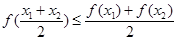 .
.
| A.①② | B.①②③ | C.③④ | D.②③④ |
函数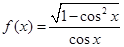 ( )
( )
A.在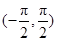 上递增 上递增 | B.在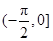 上递增,在 上递增,在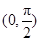 上递减 上递减 |
C.在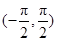 上递减 上递减 | D.在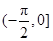 上递减,在 上递减,在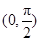 上递增 上递增 |
设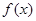 为定义域在R上的偶函数,且
为定义域在R上的偶函数,且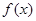 在
在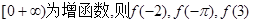 的大小顺序为( )
的大小顺序为( )
A.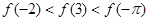 | B.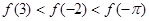 |
C. | D.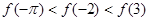 |
函数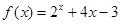 的零点所在区间是( )
的零点所在区间是( )
A.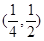 | B.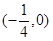 | C.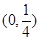 | D.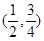 |
下列函数中,定义域是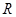 且为增函数的是( )
且为增函数的是( )
A.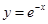 | B.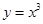 | C.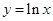 | D.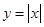 |
f(x)的定义域为R,且f(x)=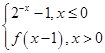 ,若方程f(x)=x+a有两个不同实根,则a的取值范围为( )
,若方程f(x)=x+a有两个不同实根,则a的取值范围为( )
| A.(-∞,1) | B.(-∞,1] |
| C.(0,1) | D.(-∞,+∞) |
对于实数x,符号[x]表示不超过x的最大整数.例如,[π]=3,[-1.08]=-2.如果定义函数f(x)=x-[x],那么下列命题中正确的一个是( )
| A.f(5)=1 |
B.方程f(x)=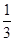 有且仅有一个解 有且仅有一个解 |
| C.函数f(x)是周期函数 |
| D.函数f(x)是减函数 |
[2013·吉林调研]已知定义在R上的函数f(x)满足f(x)+f(-x)=0,且在(-∞,0)上单调递增,如果x1+x2<0且x1x2<0,则f(x1)+f(x2)的值( )
| A.可能为0 | B.恒大于0 |
| C.恒小于0 | D.可正可负 |