题目内容
设![]() 上的两点,已知向量
上的两点,已知向量![]() ,
,![]() ,若m·n=0且椭圆的离心率
,若m·n=0且椭圆的离心率![]() 短轴长为2,
短轴长为2,![]() 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线AB过椭圆的焦点F(0,c),(c为半焦距),求直线AB的斜率k的值;
(Ⅲ)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
【答案】 解:(Ⅰ)由题意知![]()
椭圆的方程为![]()
(Ⅱ)由题意,设AB的方程为![]()
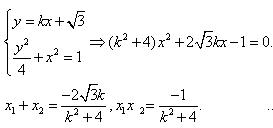
由已知![]() 得:
得:
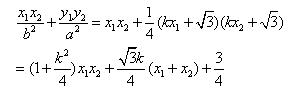
![]()
(Ⅲ) (1)当直线AB斜率不存在时,即![]() ,由m·n=0
,由m·n=0
得![]()
又 ![]() 在椭圆上,所以
在椭圆上,所以![]() ,
,
所以S =![]()
所以三角形AOB的面积为定值
(2).当直线AB斜率存在时:设AB的方程为y=kx+b
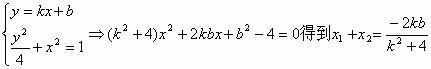 ,
,
![]()
由![]()
![]()
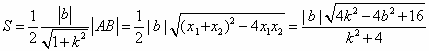
![]()
所以三角形的面积为定值.

练习册系列答案
相关题目
 上的两点,已知向量
上的两点,已知向量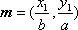 ,
,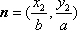 ,若
,若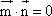 且椭圆的离心率
且椭圆的离心率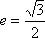 短轴长为2,O为坐标原点.
短轴长为2,O为坐标原点. 上的两点,已知向量
上的两点,已知向量 ,
, ,若
,若 且椭圆的离心率
且椭圆的离心率 短轴长为2,
短轴长为2, 为坐标原点.
为坐标原点. 过椭圆的焦点
过椭圆的焦点 (0,c),(c为半焦距),求直线
(0,c),(c为半焦距),求直线 的值;
的值; 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由. 上的两点,已知向量
上的两点,已知向量 ,
, ,若
,若 且椭圆的离心率
且椭圆的离心率 短轴长为2,
短轴长为2, 为坐标原点.
为坐标原点. 过椭圆的焦点
过椭圆的焦点 (0,c),(c为半焦距),求直线
(0,c),(c为半焦距),求直线 的值;
的值; 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.