题目内容
已和直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于A、B两点,O为坐标原点.
相交于A、B两点,O为坐标原点.
(Ⅰ)当![]() =0,0<b<1时,求△AOB的面积S的最大值;
=0,0<b<1时,求△AOB的面积S的最大值;
(Ⅱ)若![]() ,求证直线
,求证直线![]() 与以原点为圆心的定圆相切,并求该圆的方程.
与以原点为圆心的定圆相切,并求该圆的方程.
解:(Ⅰ)把![]() 代入
代入![]() ,得
,得![]() .
.
∴|AB|=![]()
∴S△AOB=-![]() ,
,
当且仅当![]() ,即
,即![]() 时取等号.
时取等号.
∴△AOB的面积S的最大值为![]() .
.
(Ⅱ)设A(![]() ),B(
),B(![]() ),
),
由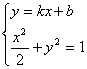 得
得![]() ,
,
∴![]() .
.
又∵OA⊥OB,
∴![]() ,即
,即![]() .
.
又![]()
![]() ,
,
∴![]() .
.
又设原点O到直线![]() 的距离
的距离![]() ,则
,则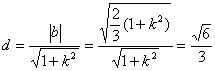
∴![]() 与以原点为圆心,以
与以原点为圆心,以![]() 为半径的定圆相切,
为半径的定圆相切,
该圆的方程为![]() .
.

练习册系列答案
相关题目