题目内容
(备用题)如图,已知椭圆
+
=1(a>b>0)上的点M(1,
)到它的两焦点F1、F2的距离之和为4,A、B分别是它的左顶点和上顶点.
(I)求此椭圆的方程及离心率;
(II)平行于AB的直线l与椭圆相交于P、Q两点,求|PQ|的最大值及此时直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
(I)求此椭圆的方程及离心率;
(II)平行于AB的直线l与椭圆相交于P、Q两点,求|PQ|的最大值及此时直线l的方程.
分析:(I)由椭圆上的点M到它的两焦点F1、F2的距离之和为4,可得a的值,再将M(1,
)代入,即可确定椭圆方程及离心率;
(II)设l的方程与椭圆方程联立,利用韦达定理确定|PQ|的表达式,从而可求|PQ|的最大值及此时直线l的方程.
| 3 |
| 2 |
(II)设l的方程与椭圆方程联立,利用韦达定理确定|PQ|的表达式,从而可求|PQ|的最大值及此时直线l的方程.
解答:解:(I)由题意,∵椭圆上的点M到它的两焦点F1、F2的距离之和为4,
∴2a=4,∴a=2
∴方程为
+
=1
将M(1,
)代入得
+
=1,∴b2=3,∴c2=1
∴椭圆方程为:
+
=1,e=
=
;
(II)∵kAB=
,∴设l的方程为:y=
x+m
由
,∴3x2+2
mx+2m2-6=0
∴△=12(6-m2)>0,∴0≤m2<6
设
,则x1+x2=-
,x1x2=
∴|PQ|=
•
=
•
=
∵0≤m2<6,∴m2=0,即m=0时,|PQ|max=
,此时l的方程为y=
x
∴2a=4,∴a=2
∴方程为
| x2 |
| 4 |
| y2 |
| b2 |
将M(1,
| 3 |
| 2 |
| 1 |
| 4 |
(
| ||
| b2 |
∴椭圆方程为:
| x2 |
| 4 |
| y2 |
| 3 |
| c |
| a |
| 1 |
| 2 |
(II)∵kAB=
| ||
| 2 |
| ||
| 2 |
由
|
| 3 |
∴△=12(6-m2)>0,∴0≤m2<6
设
|
2
| ||
| 3 |
| 2m2-6 |
| 3 |
∴|PQ|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
1+
|
|
|
∵0≤m2<6,∴m2=0,即m=0时,|PQ|max=
| 14 |
| ||
| 2 |
点评:本题考查椭圆的定义与标准方程,考查直线与椭圆的位置关系,考查弦长公式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
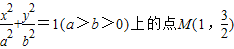 到它的两焦点F1、F2的距离之和为4,A、B分别是它的左顶点和上顶点.
到它的两焦点F1、F2的距离之和为4,A、B分别是它的左顶点和上顶点.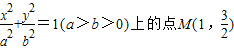 到它的两焦点F1、F2的距离之和为4,A、B分别是它的左顶点和上顶点.
到它的两焦点F1、F2的距离之和为4,A、B分别是它的左顶点和上顶点.