题目内容
在等差数列 中,
中,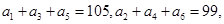 以
以 表示数列
表示数列 的前
的前 项和,则使
项和,则使 达到最大值的
达到最大值的 是( )
是( )
A.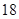 | B.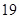 | C.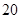 | D.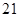 |
C
解析试题分析:因为,在等差数列 中,
中,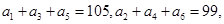 所以,由等差数列的性质,得,
所以,由等差数列的性质,得,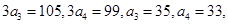 公差d=-2,
公差d=-2, ,因此,
,因此, 是递减数列,前20项为正数,从第21项起,所有项均为负数,故使
是递减数列,前20项为正数,从第21项起,所有项均为负数,故使 达到最大值的
达到最大值的 是20,选C。
是20,选C。
考点:本题主要考查等差数列的通项公式、求和公式,等差数列的性质。
点评:中档题,在等差数列中,m+n=p+q,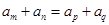 。
。

练习册系列答案
相关题目
设等差数列 的公差为
的公差为 ,若
,若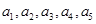 的方差为2,则
的方差为2,则 等于( )
等于( )
| A.1 | B.2 | C.±1 | D.±2 |
如果等差数列 中,
中,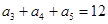 ,那么
,那么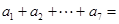 ( )
( )
| A.14 | B.21 | C.28 | D.35 |
设等差数列 的前
的前 项和为
项和为 ,若
,若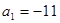 ,
,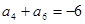 ,则当
,则当 取最小值时,
取最小值时, 等于( )
等于( )
| A.6 | B.7 | C.8 | D.9 |
等差数列的前n项和为Sn,而且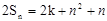 ,则常数k的值为( )
,则常数k的值为( )
| A.1 | B.-1 | C.1 | D.0 |
设S 是等差数列{a
是等差数列{a }的前n项和,S
}的前n项和,S =3(a
=3(a +a
+a ),则
),则 的值为
的值为
A. | B. | C.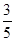 | D. |
(文科)若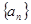 为等差数列,
为等差数列,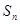 是其前n项的和,且
是其前n项的和,且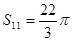 ,则
,则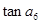 =( )
=( )
A.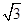 | B. | C.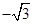 | D.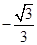 |
等差数列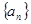 的前
的前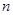 项和为
项和为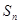 ,若
,若 ,则
,则 ( )
( )
| A.18 | B.36 | C.45 | D.60 |
 的值是
的值是 B.
B.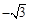 C.
C.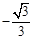 D.不确定
D.不确定