题目内容
已知函数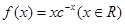
(Ⅰ)求函数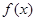 的单调区间和极值;
的单调区间和极值;
(Ⅱ)已知函数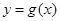 的图象与函数
的图象与函数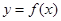 的图象关于直线
的图象关于直线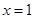 对称,证明当
对称,证明当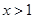 时,
时,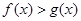
(Ⅲ)如果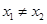 ,且
,且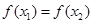 ,证明
,证明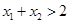
【答案】
所以f(x)在(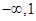 )内是增函数,在(
)内是增函数,在(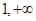 )内是减函数。
)内是减函数。
函数f(x)在x=1处取得极大值f(1)且f(1)=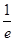
【解析】(Ⅰ)解:f’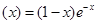
令f’(x)=0,解得x=1
当x变化时,f’(x),f(x)的变化情况如下表
|
X |
( |
1 |
( |
|
f’(x) |
+ |
0 |
- |
|
f(x) |
|
极大值 |
|
所以f(x)在(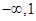 )内是增函数,在(
)内是增函数,在(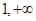 )内是减函数。
)内是减函数。
函数f(x)在x=1处取得极大值f(1)且f(1)=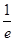
(Ⅱ)证明:由题意可知g(x)=f(2-x),得g(x)=(2-x)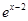
令F(x)=f(x)-g(x),即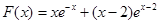
于是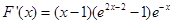
当x>1时,2x-2>0,从而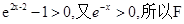 ’(x)>0,从而函数F(x)在[1,+∞)是增函数。
’(x)>0,从而函数F(x)在[1,+∞)是增函数。
又F(1)=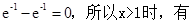 F(x)>F(1)=0,即f(x)>g(x).
F(x)>F(1)=0,即f(x)>g(x).
Ⅲ)证明:(1)
若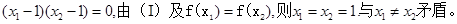
(2)若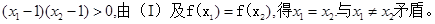
根据(1)(2)得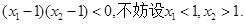
由(Ⅱ)可知,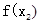 >
>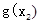 ,则
,则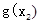 =
=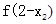 ,所以
,所以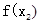 >
>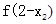 ,从而
,从而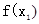 >
>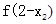 .因为
.因为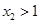 ,所以
,所以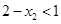 ,又由(Ⅰ)可知函数f(x)在区间(-∞,1)内事增函数,所以
,又由(Ⅰ)可知函数f(x)在区间(-∞,1)内事增函数,所以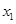 >
>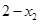 ,即
,即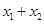 >2.
>2.

练习册系列答案
相关题目


 的定义域;
的定义域; 为何值时,函数值大于1.
为何值时,函数值大于1.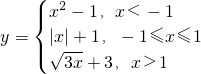 编写一程序求函数值.
编写一程序求函数值. 编写一程序求函数值.
编写一程序求函数值. 编写一程序求函数值.
编写一程序求函数值.