题目内容
【题目】如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.求:
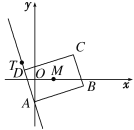
(1) AD边所在直线的方程;
(2) DC边所在直线的方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1)先由AD与AB垂直,求得AD的斜率,再由点斜式求得其直线方程;
(2)根据矩形特点可以设DC的直线方程为![]() ,然后由点到直线的距离得出
,然后由点到直线的距离得出![]() ,就可以求出m的值,即可求出结果.
,就可以求出m的值,即可求出结果.
详解:(1)由题意:ABCD为矩形,则AB⊥AD,
又AB边所在的直线方程为:x-3y-6=0,
所以AD所在直线的斜率kAD=-3,
而点T(-1,1)在直线AD上.
所以AD边所在直线的方程为:3x+y+2=0.
(2)方法一:由ABCD为矩形可得,AB∥DC,
所以设直线CD的方程为x-3y+m=0.
由矩形性质可知点M到AB、CD的距离相等
所以![]() =
=![]() ,解得m=2或m=-6(舍).
,解得m=2或m=-6(舍).
所以DC边所在的直线方程为x-3y+2=0.
方法二:方程x-3y-6=0与方程3x+y+2=0联立得A(0,-2),关于M的对称点C(4,2)
因AB∥DC,所以DC边所在的直线方程为x-3y+2=0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目