题目内容
非空数集 中,所有元素的算术平均数记为
中,所有元素的算术平均数记为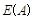 ,即
,即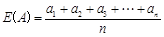 .若非空数集
.若非空数集 满足下列两个条件:①
满足下列两个条件:① ;②
;② ,则称
,则称 为
为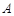 的一个“保均值子集”.据此,集合
的一个“保均值子集”.据此,集合 的“保均值子集”有( )
的“保均值子集”有( )
A.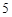 个 个 | B. 个 个 | C.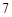 个 个 | D.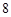 个 个 |
C
解析试题分析:非空数集A={1,2,3,4,5}中,所有元素的算术平均数E(A)= =3,
=3,
∴集合A的“保均值子集”有:{3},{1,5},{2,4},{3,1,5},{3,2,4},{1,5,2,4},{1,2,3,4,5}共7个;
故选C.
考点:本题主要考查集合的概念,学习能力。
点评:简单题,关键是理解新定义,计算元素的算术平均数。

练习册系列答案
相关题目
对于任意两个正整数m, n , 定义某种运算“※”如下:当m ,n都为正偶数或正奇数时,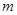 ※
※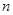 =
= 当
当 中一个为正偶数,另一个为正奇数时,
中一个为正偶数,另一个为正奇数时,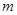 ※
※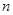 =
=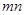 .则在此定义下,集合
.则在此定义下,集合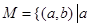 ※
※ 中的元素个数是( )
中的元素个数是( )
| A.10个 | B.15个 | C.16个 | D.18个 |
设全集U=R,A= ,B= {x|y=lg(1+x)},则下图中阴影部分表示的集合为
,B= {x|y=lg(1+x)},则下图中阴影部分表示的集合为
| A.{x|-3 <x <-1} | B.{x|-3 <x <0} |
| C.{x|-3 ≤x <0} | D.{x|x <-3} |
设集合 ,则集合
,则集合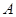 的子集个数是
的子集个数是
| A.1 | B.2 | C.3 | D.4 |
集合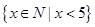 的另一种表示法是:( )
的另一种表示法是:( )
A. | B.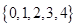 | C. | D.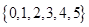 |
已知集合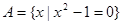 ,则下列式子表示正确的有( )
,则下列式子表示正确的有( )
① ②
②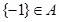 ③
③ ④
④
| A.1个 | B.2个 | C.3个 | D.4个 |
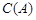 表示非空集合
表示非空集合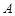 中元素的个数,定义
中元素的个数,定义
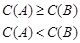 ,若
,若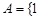 ,
,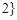 ,
,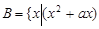
 ,且
,且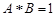 ,设实数
,设实数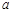 的所有可能取值构成集合
的所有可能取值构成集合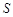 ,则
,则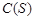 =( )
=( )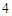

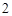
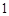
 、
、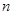 ,定义某种运算“※”如下:当
,定义某种运算“※”如下:当 ※
※ ;当
;当 .则在此定义下,集合
.则在此定义下,集合
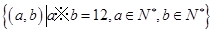 中的元素个数是( )
中的元素个数是( ) 个
个  个
个 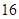 个
个 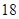 个
个