题目内容
（本小题满分12分）
已知椭圆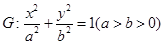
的离心率为
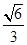，右焦点为（
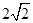,0），斜率为1的直线
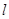与椭圆G交与A、B两点，以AB为底边作等腰三角形，顶点为
．
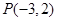（1）求椭圆G的方程；
（2）求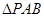
的面积．
【答案】
（1）
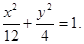（2）
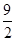
【解析】
试题分析：（1）由已知得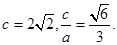
解得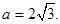
，又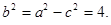
所以椭圆G的方程为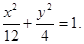
（2）设直线l的方程为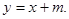
由
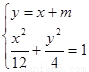得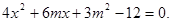
设A、B的坐标分别为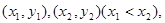
AB中点为E
，
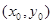则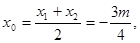
；
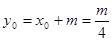因为AB是等腰△PAB的底边，所以PE⊥AB.所以PE的斜率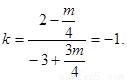
解得m=2。
此时方程①为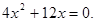
解得
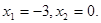所以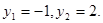
所以|AB|=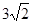
.此时，点P（—3，2）到直线AB：
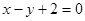的距离
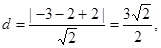所以△PAB的面积S=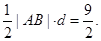
考点：本小题主要考查椭圆标准方程的求解和椭圆性质的应用.
点评：求解直线与圆锥曲线的位置关系问题，通常会直线方程与椭圆方程联立方程组，此时不要忘记验证判别式，而且运算量比较大，要仔细计算.
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
