题目内容
在 中,角
中,角 ,
, ,
,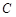 所对的边分别是
所对的边分别是 ,
,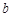 ,
,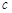 ,已知
,已知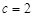 ,
,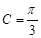 .
.
(1)若 的面积等于
的面积等于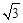 ,求
,求 ,
,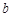 ;
;
(2)若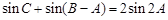 ,求
,求 的面积.
的面积.
(1)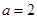 ,
, ;(2)
;(2)
解析试题分析:(1)利用余弦定理 及面积公式
及面积公式 ,列方程组就可求出
,列方程组就可求出 ,
,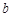 ;(2)要求三角形面积,关键在于求出边长.但已知等式条件不能直接利用正余弦定理将角化为边,所以先根据诱导公式将
;(2)要求三角形面积,关键在于求出边长.但已知等式条件不能直接利用正余弦定理将角化为边,所以先根据诱导公式将 化为
化为 再利用两角和与差的正弦公式及二倍角公式化简,得
再利用两角和与差的正弦公式及二倍角公式化简,得 ,此时约分时注意讨论零的情况.当
,此时约分时注意讨论零的情况.当 时,
时, ,
, ;当
;当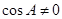 时,得
时,得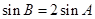 ,对这一式子有两个思路,一是用正弦定理化边,二是继续化角,
,对这一式子有两个思路,一是用正弦定理化边,二是继续化角,
试题解析:(1)由余弦定理及已知条件得, , 2分
, 2分
又因为 的面积等于
的面积等于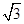 ,所以
,所以 ,得
,得 . 4分
. 4分
联立方程组 解得
解得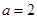 ,
, . 7分
. 7分
(2)由题意得 ,即
,即 ,
,
当 时,
时, ,
, ,
, ,
, , 10分
, 10分
当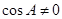 时,得
时,得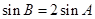 ,由正弦定理得
,由正弦定理得 ,
,
联立方程组 解得
解得 ,
, . 13分
. 13分
所以 的面积
的面积 . 14分
. 14分
考点:正余弦定理,面积公式.

练习册系列答案
相关题目
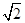 ,点M在线段PQ上.
,点M在线段PQ上.
 ,求PM的长;
,求PM的长; 中,角
中,角 ,
, ,
,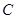 对应的边分别是
对应的边分别是 ,
,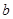 ,
,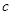 .已知
.已知 .
. ,
,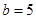 ,求
,求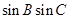 的值.
的值. 中,
中, 为定点,
为定点,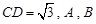 为动点,满足
为动点,满足 .
.
 与
与 的关系式;
的关系式; 的面积分别为
的面积分别为 和
和 ,求
,求 的最大值.
的最大值. 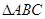 中,角
中,角 ,
,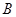 ,
,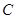 的对边为
的对边为 ,
, ,
,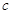 且;
且;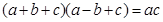
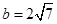 ,
,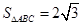 ,求
,求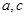 的值.
的值. 、
、 、
、 为
为 的三内角,且其对边分别为
的三内角,且其对边分别为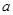 、
、 、
、 ,若
,若 .
. ,求
,求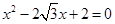 的两个根,且
的两个根,且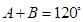 ,求△ABC的面积及AB的长.
,求△ABC的面积及AB的长.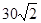 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,当甲船航行
海里,当甲船航行 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距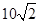 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
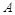 、
、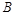 、
、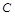 的对边分别为
的对边分别为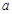 、
、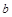 、
、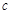 ,设S为△ABC的面积,满足
,设S为△ABC的面积,满足 .
.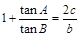 ,且
,且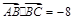 ,求
,求